Estephani TorresVillanueva
Modeling Dynamics of Massive Black Holes Using Leapfrog
CIERA REU - GalForm Group: Dr. Luke Zoltan Kelley, Claude-André Faucher-Giguère

About Estephani
My name is Estephani and I'm a rising senior completing my Bachelor's in Physics with an emphasis in astrophysics at the University of Utah in Salt Lake City.
My research at Northwestern consists of modeling black hole dynamics in realistic galactic environments using leapfrog integration and incorporating the Chandrasekhar Dynamical Friction equation along with Newtonian equations of motion.
In addition to my research at Northwestern, I have worked with Local Group Cluster Search project at my home institution to try to estimate masses and ages of star clusters in both the Andromeda (M31) and Triangulum (M33) galaxies.
Outside of research I have worked as an Outreach Coordinator for the University of Utah's Society of Physics Students (SPS) chapter and also for the Undergraduate Women in Physics and Astronomy (UWomPA). I really enjoy making physics and science accessible people from all ages. I love seeing people's natural curiosity and interest for physics and astronomy ignite when performing outreach demo shows at local K-12 schools, or even within the university campus.
As a Navy Veteran I also like to encourage and advocate for nontraditional students to not be afraid of pursuing a STEM related field or to pursue any form of higher education.
Research
Dynamical Friction
Dynamical Friction can be explained by picturing a mass M moving through a statistically homogenous distribution of particles. The gravitational field of a massive particle, accelerates the surrounding matter towards its track. Through this an overdensity forms in the backward side of its orbit resulting in the decelerating of the massive particle.
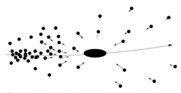
Schneider, Peter, “Extragalactic Astronomy and Cosmology. Pg 250-51
Figure 1 - The gravitational field of the large mass in this image accelerates the surrounding smaller particles towards its track. Through this process, an overdensity forms on the backend of the large mass's trajectory.
Dynamical Friction is one of the main dynamical processes that is key to the formation of massive black hole binaries (MBHBs). This process controls the orbits massive objects such as black holes and aids in the formation of black hole binaries which can create a source of gravitational waves.
A real life example of Dynamical Friction in our local galactic neighborhood are the large and small Magellanic Clouds orbiting our Milky Way galaxy.
Our Goals
Our goal is to create an enhanced cosmological simulation which can more accurately depict massive black hole dynamics in realistic galactic environments by using leapfrog integration and by incorporating methods from the literature of Binney & Tremaine (1987) along with Newtonian equations of motion. We also try to understand how dynamical friction affects massive black holes and the background particles that surround it. One step we take to accomplish this is by analyzing how the impact parameter of surrounding particles affects the angle of deflection of those same particles as they interact with the gravity of our massive black hole.
Our Methods
The methods we use to achieve an enhance cosmological simulation are the leapfrog integration equations along with the Binney & Tremaine (1987) methods of finding a particles' angle of deflection as it travels by our massive object (i.e. Massive Black Hole). The leapfrog method of integration is similar to the Euler method, however, leapfrog integration allows for the continual updating of positions and velocities of particles at interwoven time steps such that the velocity and position values skip or leapfrog over one another. We still use Euler methods however, but only as a way of verifying that our simulation is working properly. Leapfrog integration is extremely useful in hydrodynamic simulations, since the acceleration values in gravity simulations depend on only the positions of the gravitating masses. Additionally, this method, conserves both energy and angular momentum of the dynamical systems being studied.
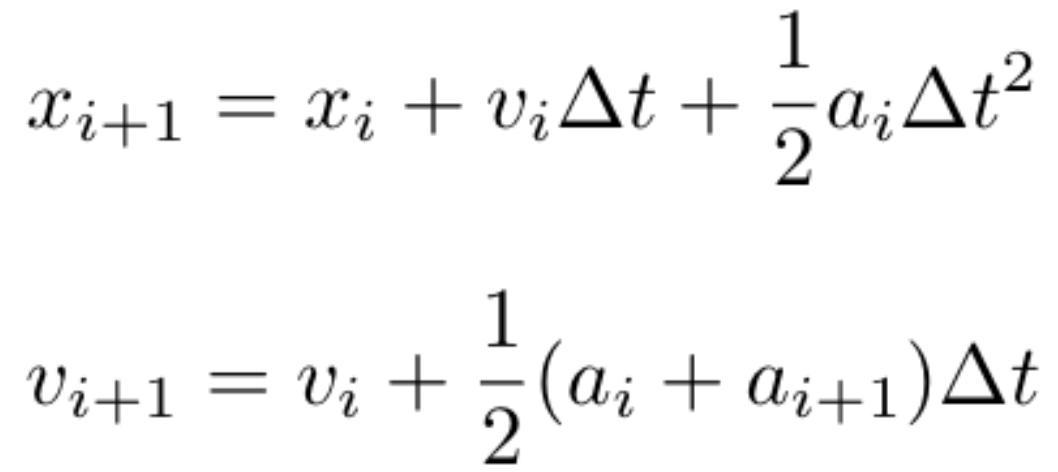
Figure 2 - Leapfrog equations for updating positiong and velocity of particles.
Once we have particle positions and velocities, we can plot their trajectories and analyze how their paths are affected by the massive black hole. One way in which we do this is by analyzing the angle of deflection for each particle at different impact parameters. Since we initialized our velocity for each particle as well as the initial position (i.e. impact parameter) we can easily calculate the angle of deflection produced by our simulation by using the Binney & Tremaine methods as well as by fitting a curve to our particle trajectory.
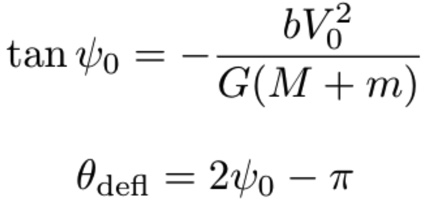
Figure 3 - Binney & Tremaine 1987 equations for calculating particle angle of deflection.
Results
After obtaining the positions in both x and y directions for our particles while using both Leapfrog and Euler methods, we plot our particle trajectories to ensure that they are following a physically correct path past the massive object. In this situation, we plotted a small sample of 10 particles and we show the effects of imposing different impact parameters on each of these background particles as they travel along their trajectory past the larger mass. We conclude that our simulation is working correctly based on the similarity of the trajectories produced from both Leapfrog and Euler methods.
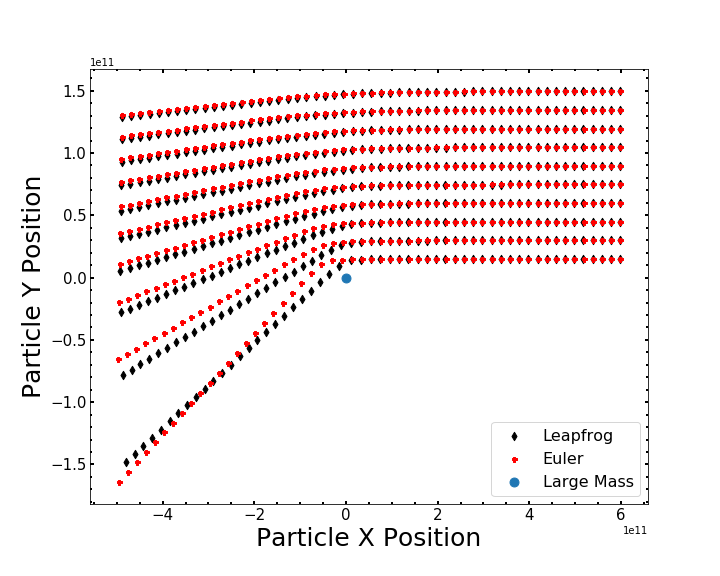
Figure 4 - The trajectories of each particle with different impact parameters. The trajectories from Leapfrog method results are shown by the black diamond markers and the trajectories for the Euler method results are shown by the red dots. The blue point represents the location of the massive black hole.
With confirmation that our small simulation is functioning properly, we proceed to analyze the normalized fractional energies of each particle in the simulation over an array of time step sizes (Δt). We perform this process for both Leapfrog and Euler methods to confirm that by using Leapfrog there is a better conservation of energy. Figure demonstrates why using Leapfrog integration is ideal for gravity simulations, since the fractional errors in energies are almost 5 orders of magnitude smaller than the errors produced from using Euler integration.
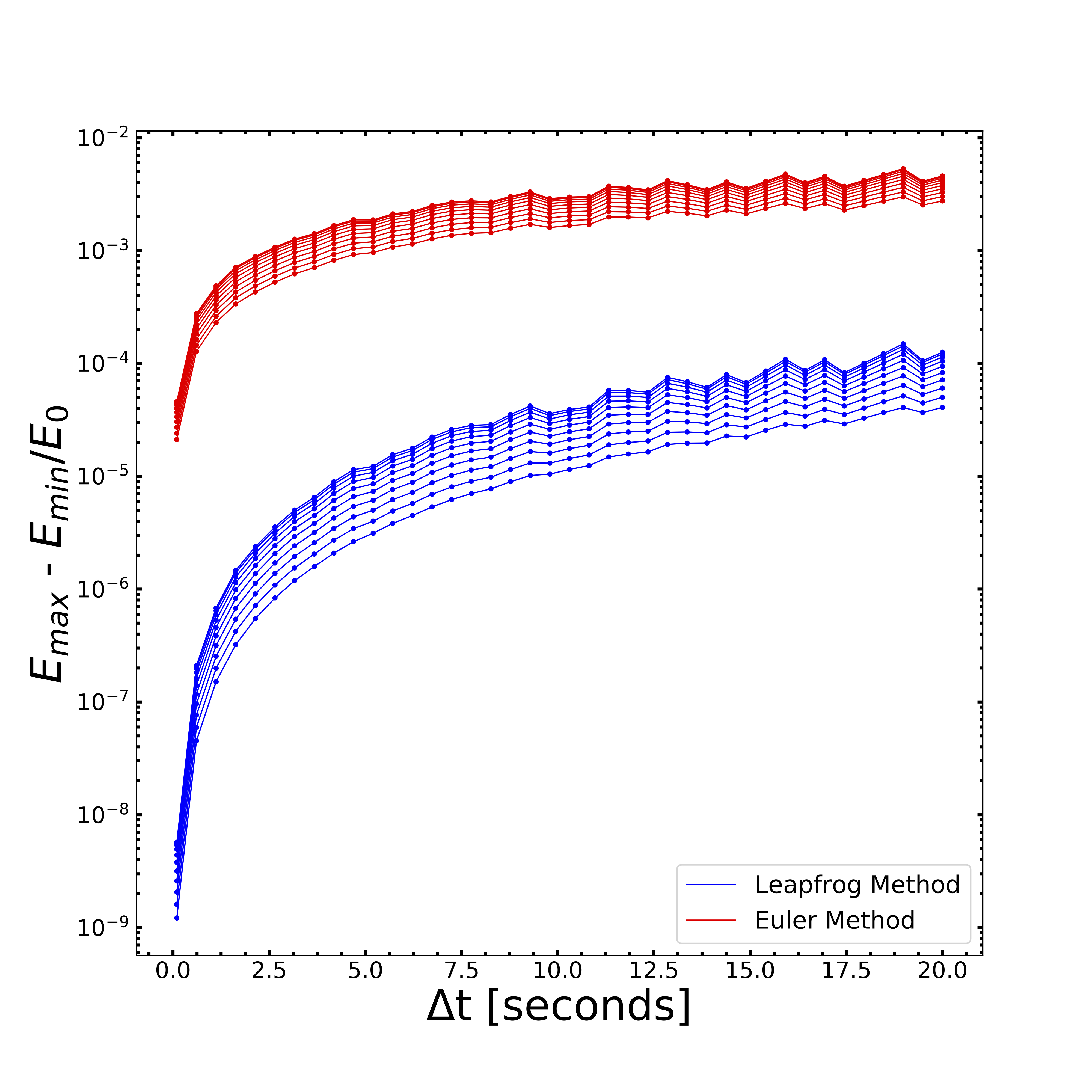
Figure 5 - Normalized fractional energies for both Leapfrog (blue) and Euler (red) methods over an array of timesteps (Δt). Although results from both methods follow a similar curve, we chose to generate our simulations via the Leapfrog method due to the lower (~5 orders of magnitude) fractional errors in energies.
Knowing that our simulation is functioning properly we proceed to deriving angles of deflection. To be able to analyze the dynamical friction enacted on the large mass we need to first look at the varying impact parameters from each particle and the angle of deflection. We begin by measuring the angle of deflection for the particle with the smallest impact parameter to the massive object. We employ the use of curvefit functions and to find the angle of deflection produced by our simulation. The results of this method are shown in figure 6 for both Leapfrog and Euler integrations.
One last thing we want to observe is how the angle of deflection changes as a we change the time step (Δt) and also how accurately it matches the angle value we obtain from using the Binney & Tremaine equations from figure 3.
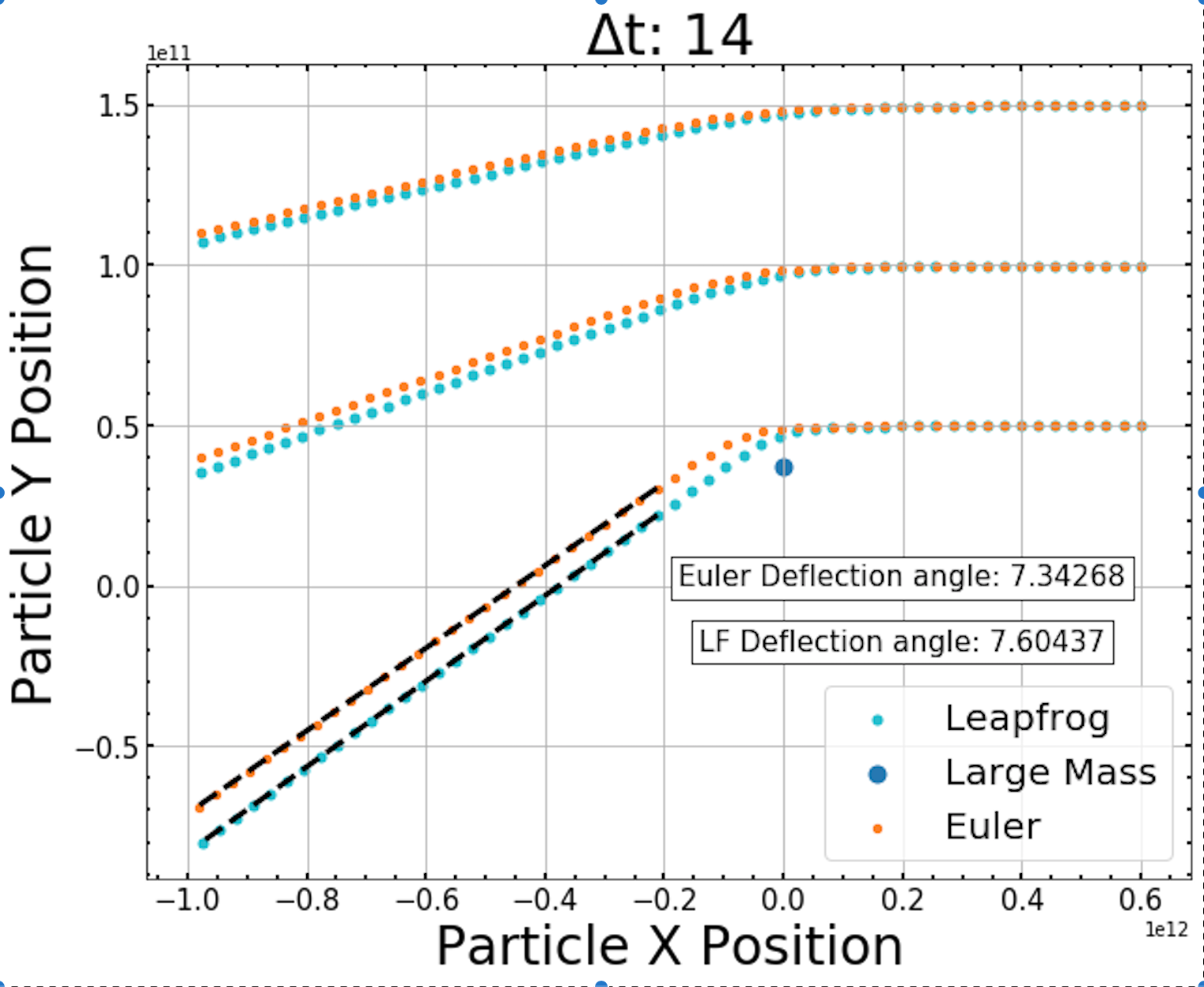
Figure 6 - The curvefit method angle value is shown in the plot above for both Leapfrog (cyan) and Euler (orange) integration methods. We compare these values to the Binney & Tremaine (1987) value of 7.613º which is calculated using the initial velocity and the impact parameter of the particle with the closest trajectory to our massive object (blue point).
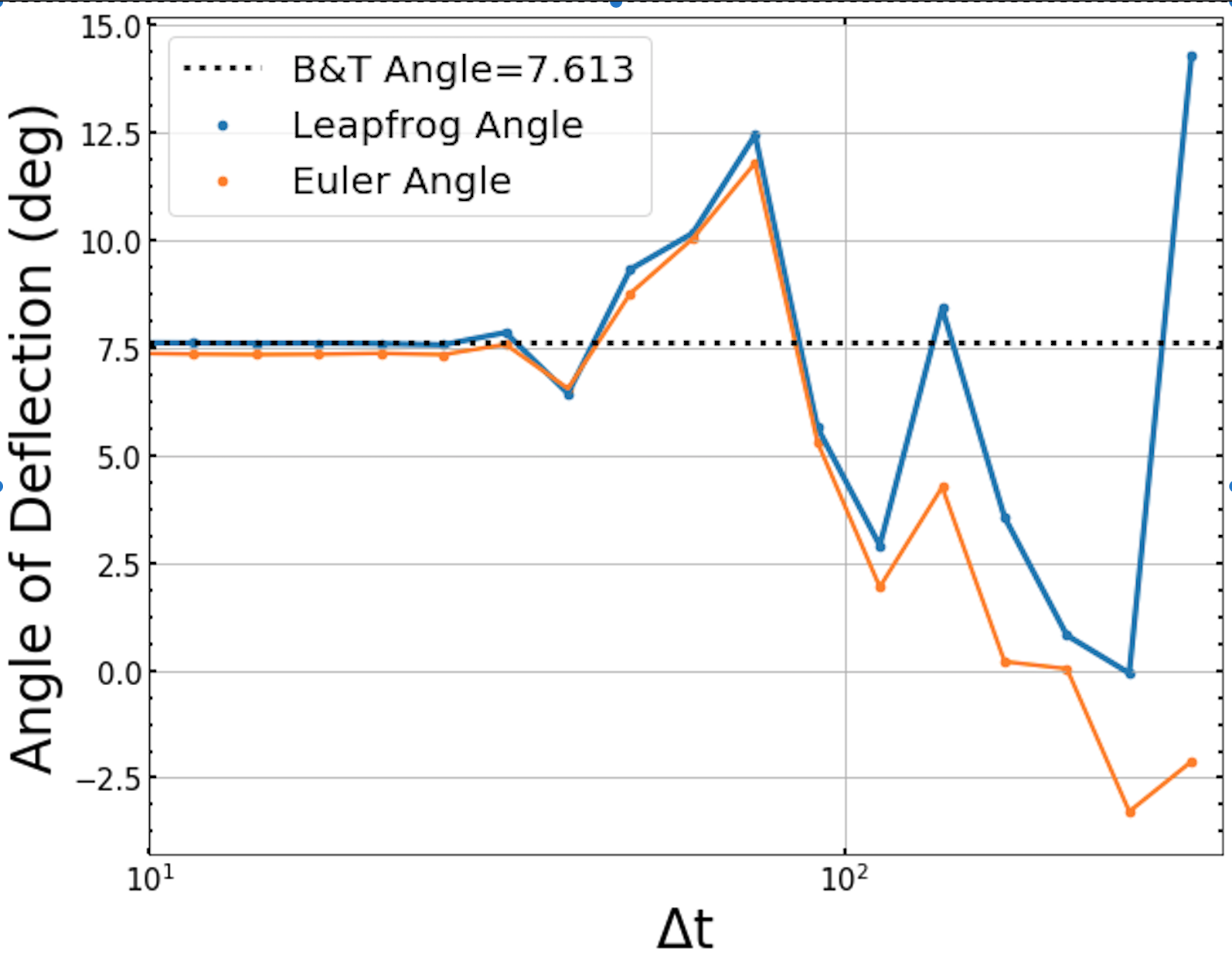
Figure 7 - The figure above shows the angle of deflection values calculated using the curvefit method for Euler (orange) and Leapfrog (blue) integration over an array of timesetps (Δt). The Binney & Tremaine value is represented by the black dashed line. We can conclude from this figure that the Binney & Tremaine angle value matches the leapfrog method angle value more closely than the Euler method.
Conclusions
By comparing the results we obtain for particle postions, velocities, and energies from the Leapfrog integration to the results form the Euler method of integration, we can conclude that our simulation is working appropriately and incorportating all the needed forces and gravitational effects on both the background particles and the large mass itself. We can also conclude that our simulation produces correct particle trajectories and angles of deflection as they pass by the larger mass by comparing the angle of deflection values calculated using the curvefit method to the values derived from the Binney & Tremaine 1987 values. Finally we confirm that the use of the Leapfrog method of integration in simulations leads to a better physical representation of black hole and background particle dynamics by minimizing the error in both the particle trajectories and energies.
Future Work
With confirmation that our simulation is working correctly, our next steps will be to combine our results from the particle trajectories and energies to calculate the Chandrasekhar Dynamical Friction (Am) from the literature and compare this to the simulated Dynamical Friction. We want to be to able to broaden this simple simulation to be able to model the effects of the large mass on the background particles and vice versa in all 3 dimensions. Currently, all of the simulated small particles have the same initial conditions, but we want to enhance our simulation by providing different initial conditions for every particle to more accurately depict real like interactions between black holes and their surrounding medium. Finally, once we have added these elements to our simulation, we want to incorporate our models into larger and broader hydrodynamical simulations.
References
Abbott, B., Abbott, R., Abbott, T., et al. 2016 Physical Review Letters, 116, doi:10.1103/physrevlett.116.061102.http://dx.- doi.org/10.1103/PhysRevLett.116.061102
Binney, J., & Tremaine, S. 1987, Galactic Dynamics
Kelley, L. Z., Blecha, L., & Hernquist, L. 2017, Monthly Notices of the Royal Astronomical Society, 464,3131–3157. http://dx.doi.org/10.1093/mnras/stw2452
P. Schneider. 2006, Extragalactic Astronomy and Cosmology, Springer Berlin Heidelberg, Berlin, Heidelberg
Sijacki, D., Vogelsberger, M., Genel, S., et al. 2015, Monthly Notices of the Royal Astronomical Society, 452,575–596. http://dx.doi.org/10.1093/mnras/stv1340