Welcome! My name is Rachel Hur and I am a physics undergraduate entering my last year at the University of Oregon. I began research at my home institution with Dr. Ben Farr, primarily working on developing a Bayesian method for characterizing instrumental glitches that appear in gravitational wave detectors. This summer, I have been fortunate enough to get the chance to work with Dr. Vicky Kalogera and others in extending the capabilities of binary stellar evolution/population synthesis codes. Since beginning my research experiences, I have also developed an interest and appreciation for our ability to constrain our story of the evolution of the universe and its constituents, its connection to our understanding of particle physics, and right within this intersection, the dark matter hypothesis.
Outside of research, in my spare time I enjoy practicing Brazilian Jiu-jitsu, camping, and riding my bicycle.
When two gravitationally bound stars get close enough to one another, they can exchange mass due to a variety of mechanisms including supernova explosions, stellar winds, and Roche-lobe overflow. These mass transfer mechanisms in close binaries provide theoretical explanations of detectable astrophysical signatures such as X-ray emission, neutron star spin-up, Type 1A supernovae, and changes in orbital separation. In general, mass transfer can significantly change our expectations of the formation, evolution, and thus, final fate of two stars in a binary.
The theory of mass transfer in circular orbits have been well understood for decades (Paczynski 1971) and most binary population synthesis codes (including StarTrack, BSE, binary_c and SeBa reflect this: once an eccentric binary system enters a mass transfer phase, the orbits are assumed to circularize almost immediately, and equations for mass transfer in circular orbits can be used. This decision has been motivated by astrophysical theory, and also convenience: the dissipative effect of tidal forces between the two objects are thought to be efficient enough to instantaneously circularize the orbit, and all other contributions to changes in eccentricity are assumed to be negligible. Additionally, developing a formal, analytical approach to mass transfer in eccentric orbits is a non-trivial task due to complicated dynamics present in eccentric orbits.
On the other hand, there exist observations of binaries with non-zero (and sometimes, significantly high) eccentricity, including observations of high-mass X-ray binaries (Raguzova & Popov 2005), semi-detached binary systems (Petrova & Orlov 1999), and post-AGB binaries (van Winckel 2003) which directly conflict with the assumption of instantaneous tidal circularization. Moreover, theory suggests that mass transfer from mechanisms such as supernova kicks/mass-loss and Roche-lobe overflow could significantly compete with, or enhance the effects of, tidal forces. There is a missing piece of theory that can simultaneously enhance modern stellar evolution tools and possibly explain the known populations of eccentric, mass-transferring binaries as well as observed eccentric binaries that are thought to have passed through a mass transfer phase (such as the blue stragglers described in Geller & Mathieu 2011)
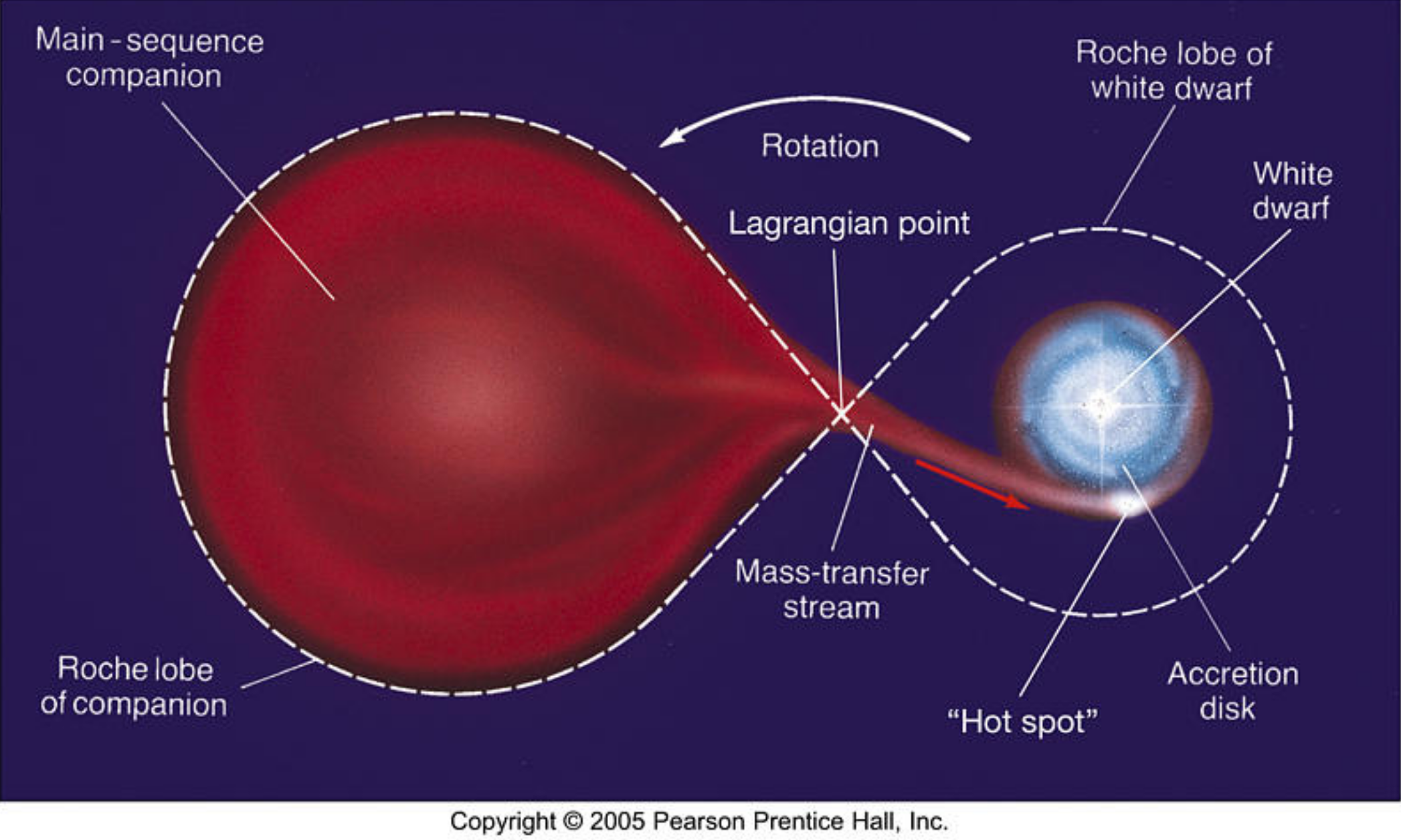
The diagram below describes the classic Roche lobe overflow mass transfer mechanism. The Roche lobe of each star traces out the critical gravitational equipotential at which orbiting gas and material is bound to that star. The inner Lagrangian point is a point of unstable equilbrium, so as the donor star (red) evolves and swells up, the moment it reaches the critical Roche lobe equipotential, mass begins to eject from the donor at the Lagrangian point and the other accreting star begins to grow in mass.
We decide to use the analytical model for eccentric Roche lobe overflow mass transfer described and derived in detail in Dosopoulou & Kalogera 2016a and Dosopoulou & Kalogera 2016b, hereafter termed Paper 1 and Paper 2. We direct the interested reader to these papers, and give a brief overview here.
The analytical treatment models mass transfer as a perturbation to the 2-body system, where mass is transferred instantaneously at periastron (the point at the two bodies are closest to one another). This treatment is useful because it also allows for general (and physically real) case of nonconservative mass transfer, meaning that some of the mass that is ejected by the donor, leaves the system entirely, and takes away some portion of angular momentum away with it.
They show that all 6 Keplerian elements, or, the "orbital elements" which completely describe the binary level
properties,
remain constant (or get integrated out) except for the orbital separation a, eccentricity e.
For the sake
of running simple initial tests, we consider a compact object (point mass) accretor and a non-degenerate star.
Then, the orbit averaged (or, "secular") differential equations describing the binary evolution (Eqns 43 and 44
in Paper 2)
reduce to:
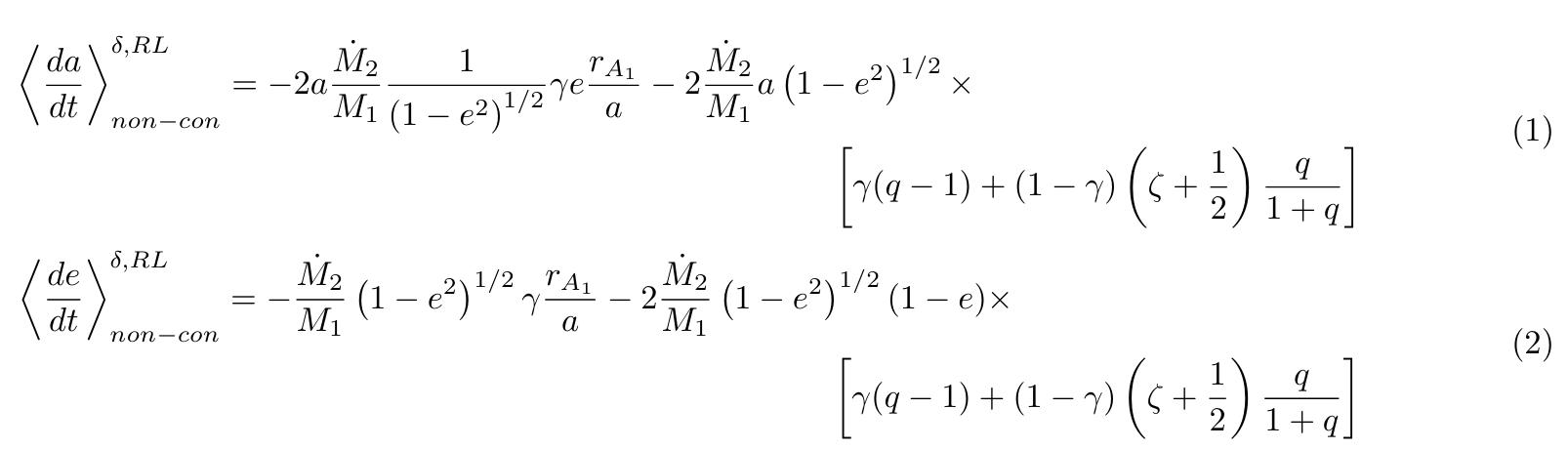where M1, M2 are the masses and subscripts 1 and 2 refer to the donor and accretor,
respectively;
q is the mass ratio M1/M2; rA1 is the distance from the center of
mass of
the donor to the point of ejection; and γ is the mass transfer efficiency for non-conservative mass loss
defined
by Ṁ2 = - γ Ṁ1. Lastly, ζ describes the
orbital
angular momentum lost as a fraction of mass loss, defined by J̇/J = - γ Ṁ/M, where J is the
orbital
angular momentum and M=M1+M2 is the total mass of the system.
MESA first calculates the derivative of the orbital angular momentum, J̇ then the other binary properties like orbital separation a and eccentricity e are calculated from this quantity. To calculate J̇ they assume that for nonconservative mass transfer, ζ (as defined above) is given by the fast wind mode ζ = M2/M1 and then also allow mass to also be lost through isotropic re-emission of the accretor ζ = M1 / M2. Plugging these in to the equation for nonconservative mass transfer below
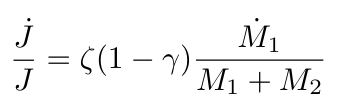
we can derive Eqn 5 in Paxton et al.1 However, the secular equations (1) and (2) are derived for a, not J. Thus, we re-express the secular equation using the canonical orbital evolution equation below
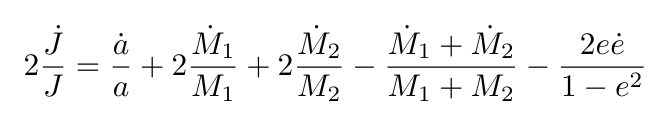
We have implemented these equations into MESA using the run binary extras hook in MESA,
allowing for both the fast wind and isotropric re-emission prescriptions above.
When running our initial tests for various low mass configurations, we turn off tidal cirularization (in order to allow systems to keep a non-zero eccentricity by the time they enter the mass transfer phase). The initial tests were unfruitful; the time step continuously decreases until hitting an unreasonably small scale, causing the MESA to stop evolving. After some investigation, we learned that MESA first evolves each individual star at each time step using a higher order Runge-Kutta integration, then the differential equations governing binary interactions are evolved at each time step using the Euler integration method. Normally, this latter integration method does not yield stable solutions, however, we are not yet certain if this is the cause for these errors. We have tested that direct integration of the coupled secular equations (1) and (2) using a 4th order Runge-Kutta integration method, where mass transfer rate is kept constant, does not suffer from numerical issues. We plan to continue to investigate the cause for these errors, and upon completion of this new tool, apply the MESA-dependent POSYDON framework for exploring population synthesis applications.
I would like to thank Vicky Kalogera, Aaron Dotter, Jeff Andrews, and Kyle Rocha, as this research would not have been possible without their guidance and support.
This material is based upon work supported by the National Science Foundation under grant No. AST-1757792.