Computational ecology is a growing field that provides insight into the nature of ecological communities. Increasing our knowledge of biological competition can aid researchers in understanding the nature of potential living communities in the universe. We consider communities exhibiting cyclic competition among three competing species analogous to the children’s game of Rock-Paper-Scissors (RPS). Modern applications of computational ecology can be found in studies on competition between different strains of influenza (1) as well as bacterial RPS communities (2, 3). There is much that is unknown regarding the limit and extent such communities, thus there is active research within developing these models even further.

In order to model these competition models, we first created an improved Euler numerical solver using Python. Using this solver as a tool, we input three coupled differential equations based on a special case of the models present in (4), including a new saturation term, to obtain the output of the models. Key coefficients include the inter-species competition coefficient α and the saturation coefficient A. The saturation term physically represents the limit of inter-species competition. i.e., the inter-species competition does not grow indefinitely with population but levels off at a fixed value.

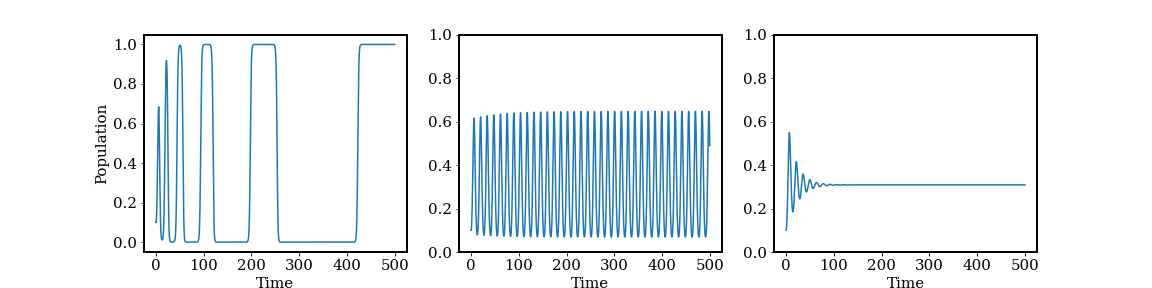
For the α = 1.5 case there is coexistence for all saturation values greater than 0, and the coexistence values now depend on A. However, the solution output for α = 3.0 shifts from a heteroclinic cycle (small A), to a transition regime of periodic solutions (Hopf regime - intermediate A), to stable coexistence (large A). The Hopf regime is particularly fascinating as previously only the coexistence and heteroclinic regimes had been found (except exactly for α = 2). We find the Hopf/heteroclinic transition occurs approximately when α/(1+A) = 2, i.e., the heterolinic cycle occurs when the effective interspecies competition cofficient is 2 and the Hopf regime eats into what would be the stable coexistence regime. Thus, for α = 3 the heteroclinic/Hopf transition occurs for A ≈ 0.5 .

LinkedIn

Email: dylantchambers [at] gmail.com

[1] A. Dimas Martins, E. Gjini, Modeling competitive mixtures with the Lotka-Volterra framework for more complex fitness assessment between strains, Front. Microbiol. 11 (2020) 2132.

[2] B. Kerr, M. A. Riley, M. W. Feldman, B. J. M. Bohannan, Local dispersal promotes biodiversity in a real-life game of rock-paper-scissors, Nature 418 (2002) 171–173.

[3] B. C. Kirkup, M. A. Riley, Antibiotic-mediated antagonism leads to bacterial game of rock-paper-scissors in vivo, Nature 428 (2004) 412–414.

[4] R. M. May, W. J. Leonard, Nonlinear aspects of competition between three species, SIAM J. Appl. Math. 29 (1975) 243–253.

[5] A. Bayliss, A. Nepomnyashchy, V. A. Volpert, Beyond rock−paper−scissors systems − deterministic models of cyclic ecological systems with more than three species, Physica D 411 (2020) 132585.

This material is based upon work supported by the National Science Foundation under Grant No. AST-2149425, a Research Experiences for Undergraduates (REU) grant awarded to CIERA at Northwestern University. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.