Investigating the Effect of Neutrino Decay on Flavor Oscillations
Background
As our knowledge of neutrinos has grown throughout the latter half of the 20th century and into the 21st century, so has the number of open
questions in neutrino physics. For example, we now know that neutrinos are massive particles which oscillate between three different flavor
states, but we can not precisely predict how they will oscillate (de Gouvêa 2008)
The three flavor states which a neutrino can oscillate between are referred to as electron-type, muon-type, and tau-type neutrinos
(de Gouvêa 2008). While we
want to know how any given neutrino will oscillate over time, only the electron-type antineutrinos are visible to reactor neutrino detectors (de Gouvêa 2008),
so we focused on how the probability that a neutrino will remain an electron-type neutrino changes over time. Here, we investigated the
effects of the decay of the different neutrino mass eigenstates on neutrino flavor oscillations. We then determined potential bounds on the
lifetimes of our neutrinos in a long-baseline reactor neutrino experiment and looked for correlations between the neutrino lifetimes
and the variables which parameterize the flavor oscillations, assuming the data are consistent with infinite neutrino lifetimes.
The JUNO Experiment
Neutrino flavor oscillations, or oscillations of the probability of finding an electron-type neutrino, are driven by four parameters:
Δ m 221, Δ m231, sin 2θ12, and sin 2θ13,
where Δm2ij are the mass-squared differences between mass-states νi and νj and θ12
and θ13 are the lepton mixing angles. Δm231 and sin2θ13 drive short,
fast neutrino oscillations, while Δm221 and sin2θ21 drive long oscillations (de Gouvêa 2008).
Currently, no neutrino detectors exist which can observe both the long and short oscillations (An et al. 2015). However, the Jiangmen Underground Neutrino
Observatory (JUNO), which is under construction, will have the capability to detect both types of oscillations. JUNO will have a long
baseline of 52 km, allowing it to detect the long oscillations, as well as high resolution, which will enable it to observe the small
oscillations(An et al. 2015). Our research consists of simulating data to be collected by the JUNO experiment.
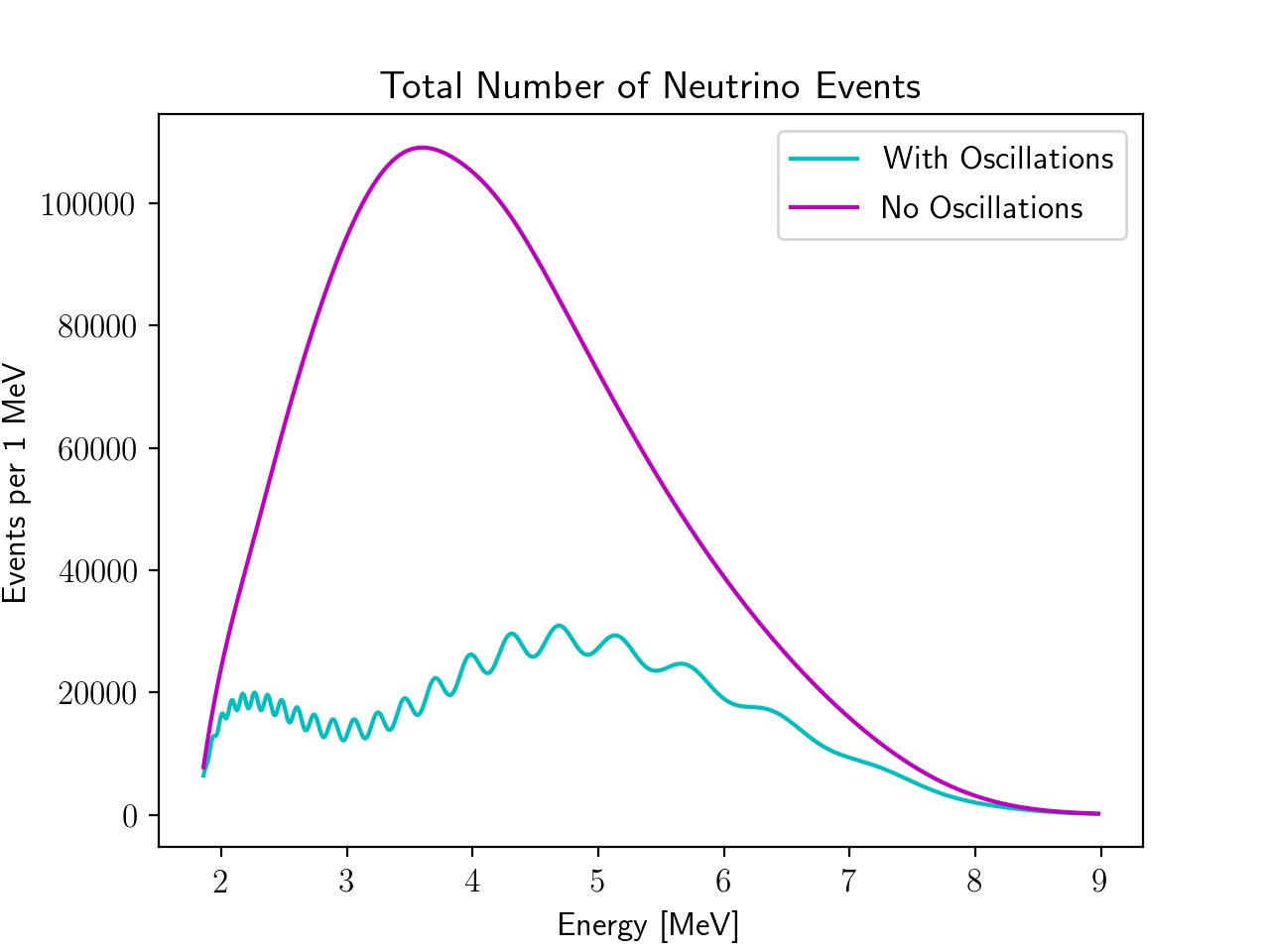
The JUNO experiment will be able to detect over 100,000 electron antineutrino events over the span of 5-10 years (An et al. 2015), and we sought to model
this in our research. The total number of neutrino events is given by the product of the probability of finding an electron-type neutrino,
the neutrino cross section, and the neutrino flux at the detector(de Gouvêa 2008).
We obtained the neutrino cross section as a function of antineutrino energy from Strumia & Vissani (2003).
The neutrino flux, in arbitrary units, is determined by the ratio of isotopes which produce the neutrinos multiplied by the isotope spectra
(Mueller et al. 2011). We determined the spectra according to the methods outlined in
Mueller et al. (2011), and we used the isotope ratios for neutrinos detected by JUNO, which are 57.7% 235U, 7.6% 238U, 29.5% 239Pu, and
5.2% 241 Pu (An et al. 2015). The neutrino cross section and neutrino flux expected for JUNO experiments
are shown as a function of antineutrino energy in the figures below.
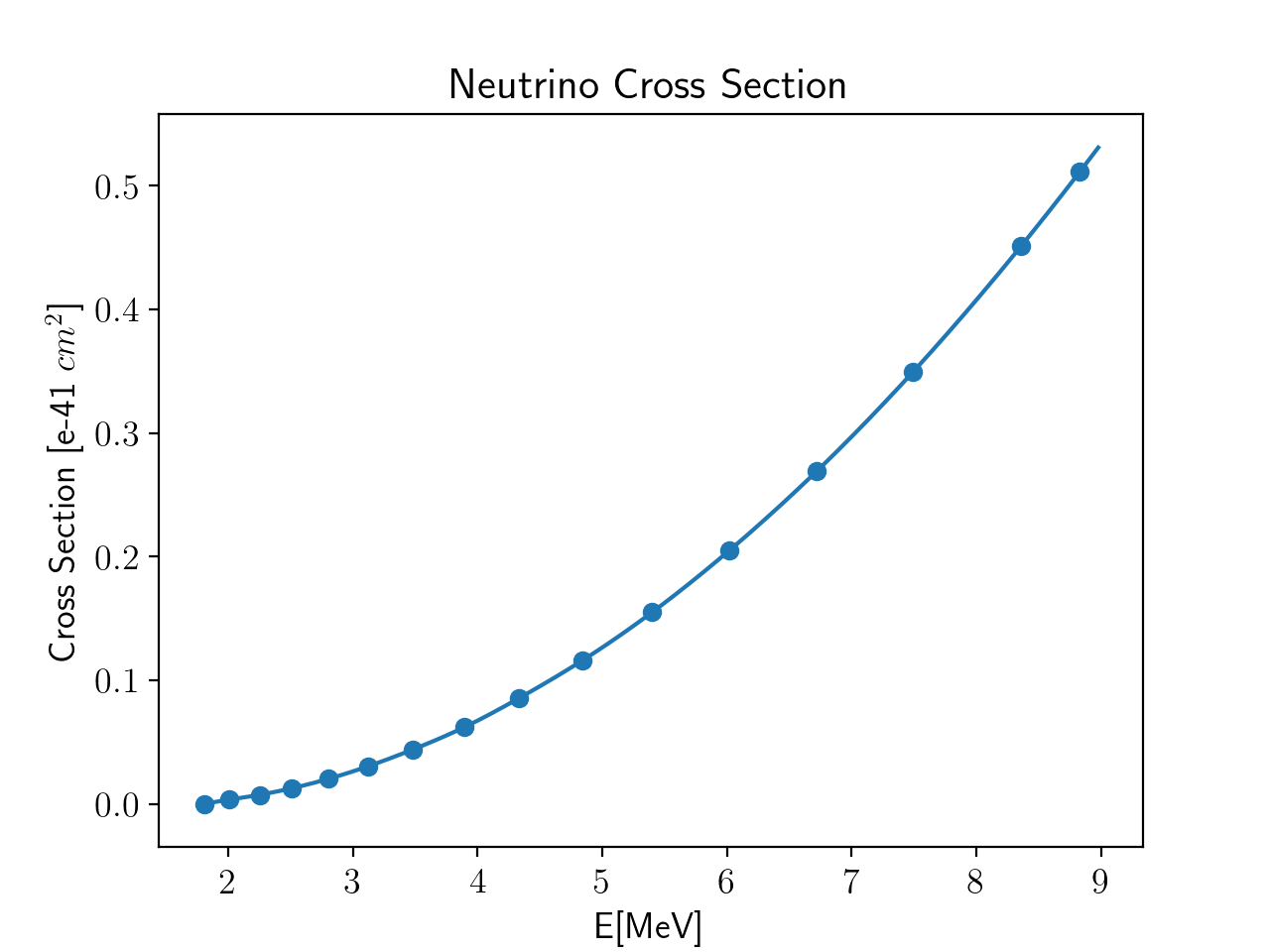
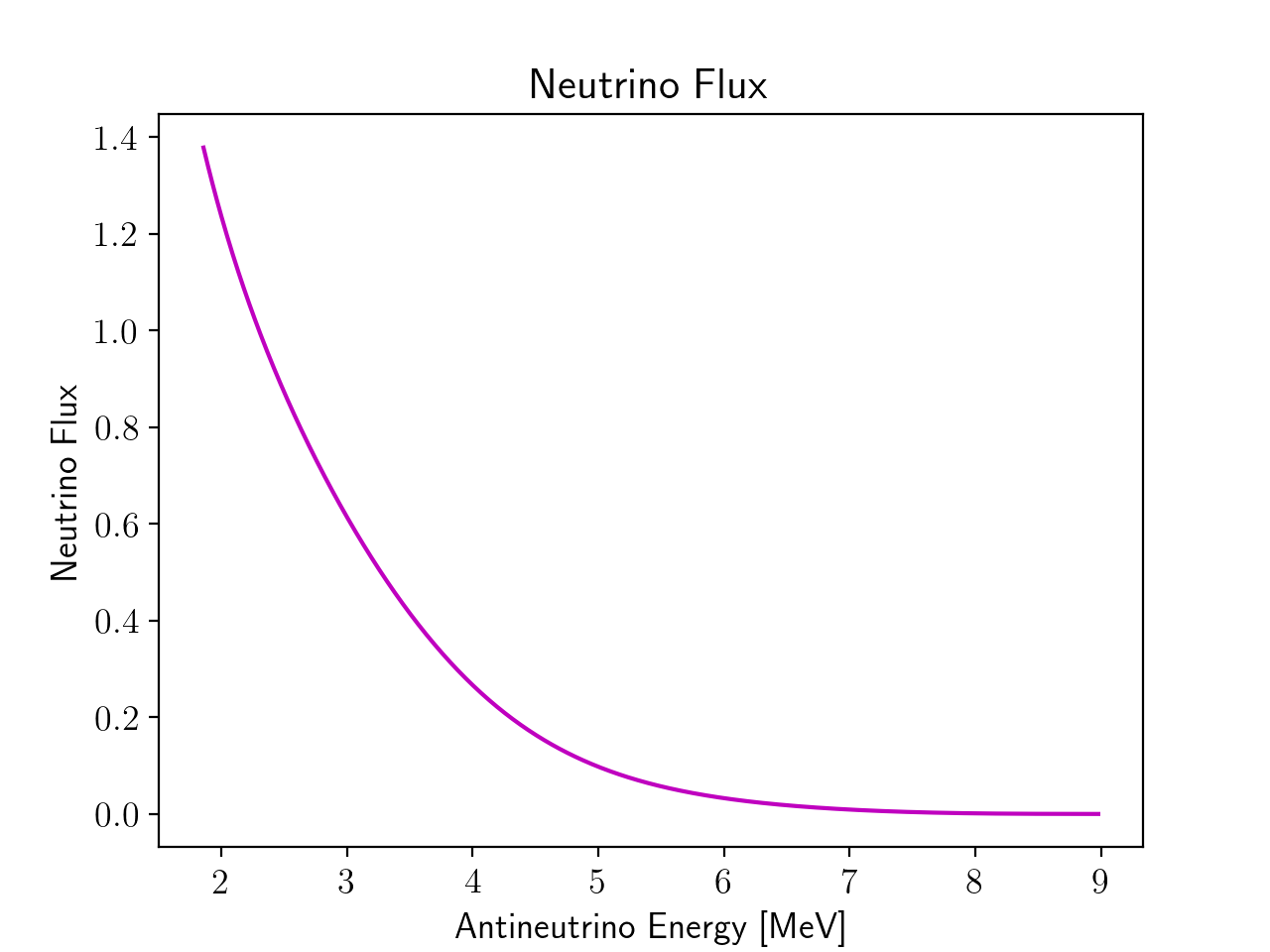
The product of the neutrino cross section and the neutrino flux as a function of antineutrino energy represents the total number of neutrino events when there are no flavor state oscillations. This quantity multiplied by the probability function gives the total number of neutrino events with oscillations. We normalized our data sample to 100,000 events in the case where oscillations occur, which is around 5 years of JUNO data. Both cases are shown in the figure to the right.
Neutrino Decay
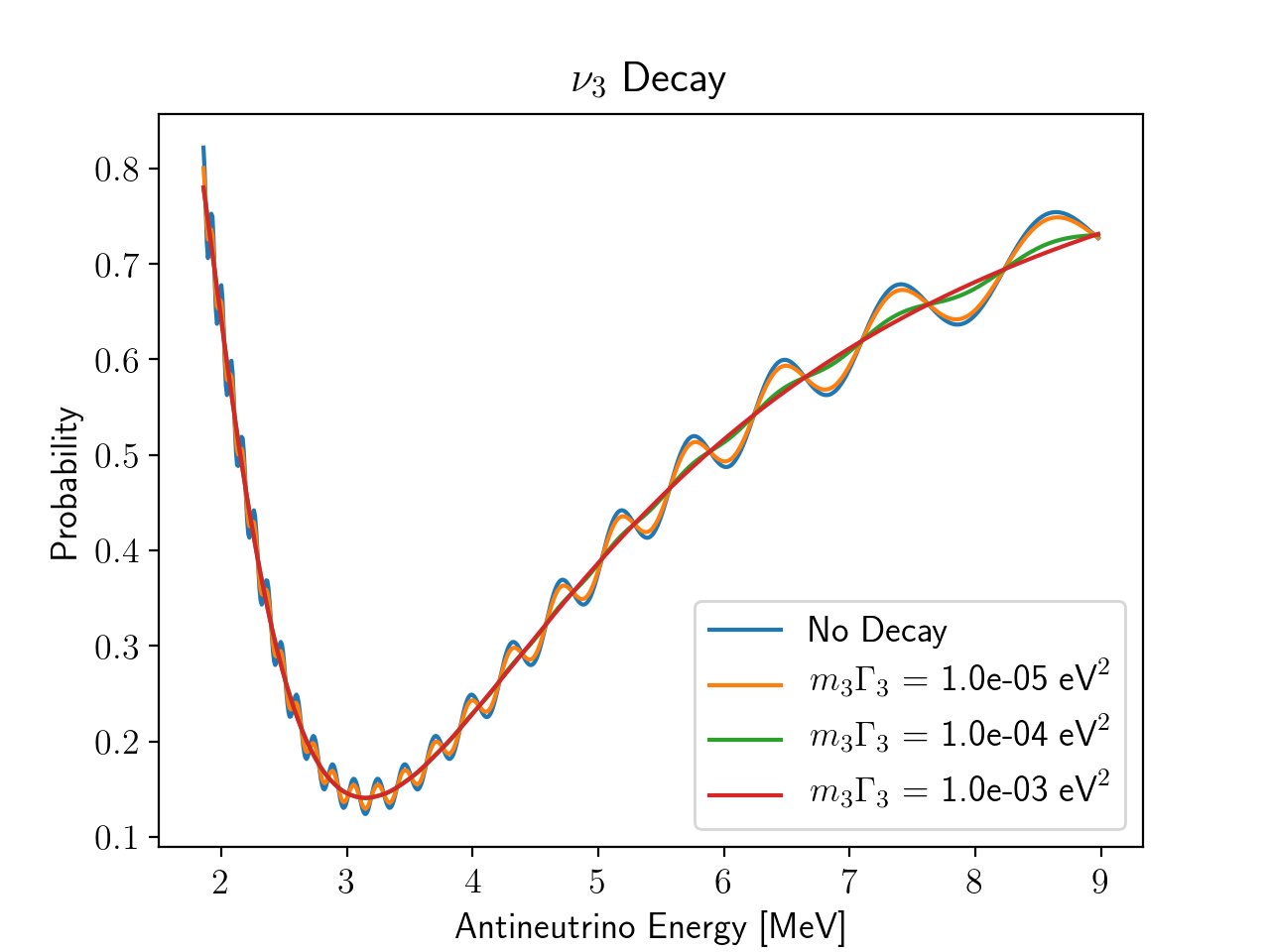
We first let each of the three neutrino mass eigenstates, ν1, ν2, and ν3, decay one at a time, and then we let multiple neutrino states decay. In each case, we assumed the daughter particles were not visible to the detector. As can be seen from the figures below, ν3 decay suppresses the small oscillations, ν2 decay suppresses the long oscillations, and ν1 roughly reduces the overall number of neutrino events. The hybrid cases, in which we allowed multiple neutrinos to decay, show multiple decay effects, from which it can be deduced which neutrinos decayed.
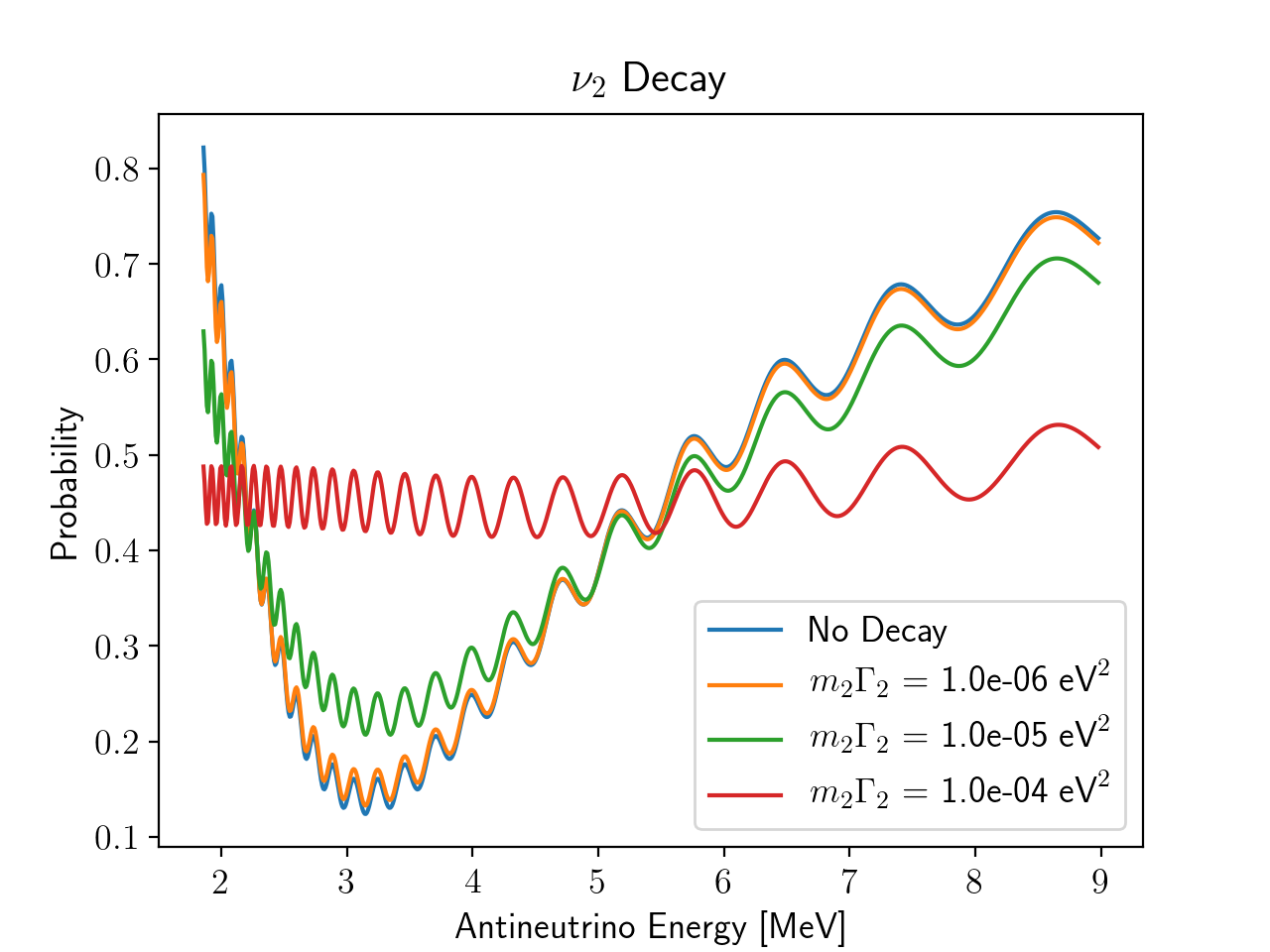
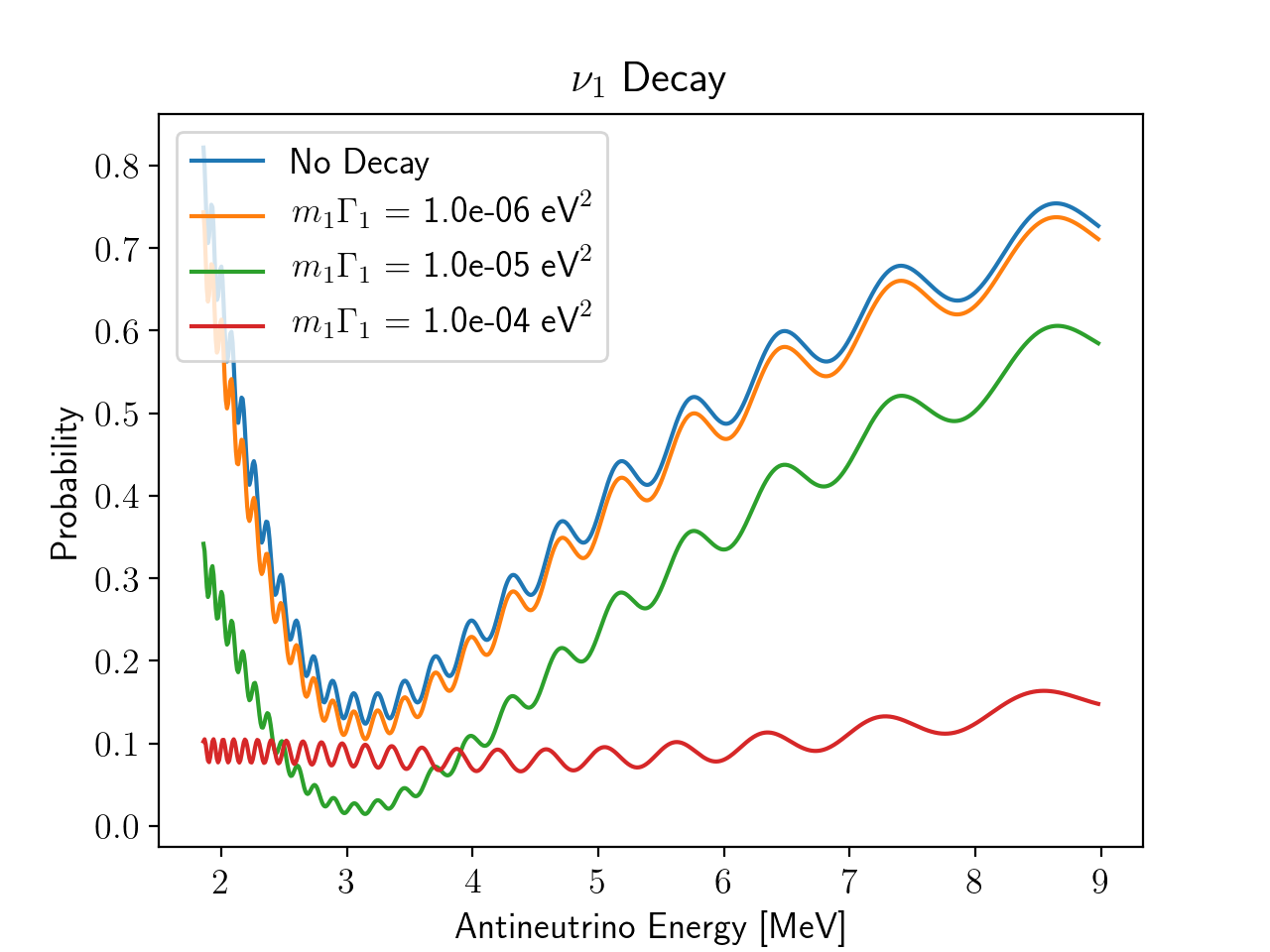
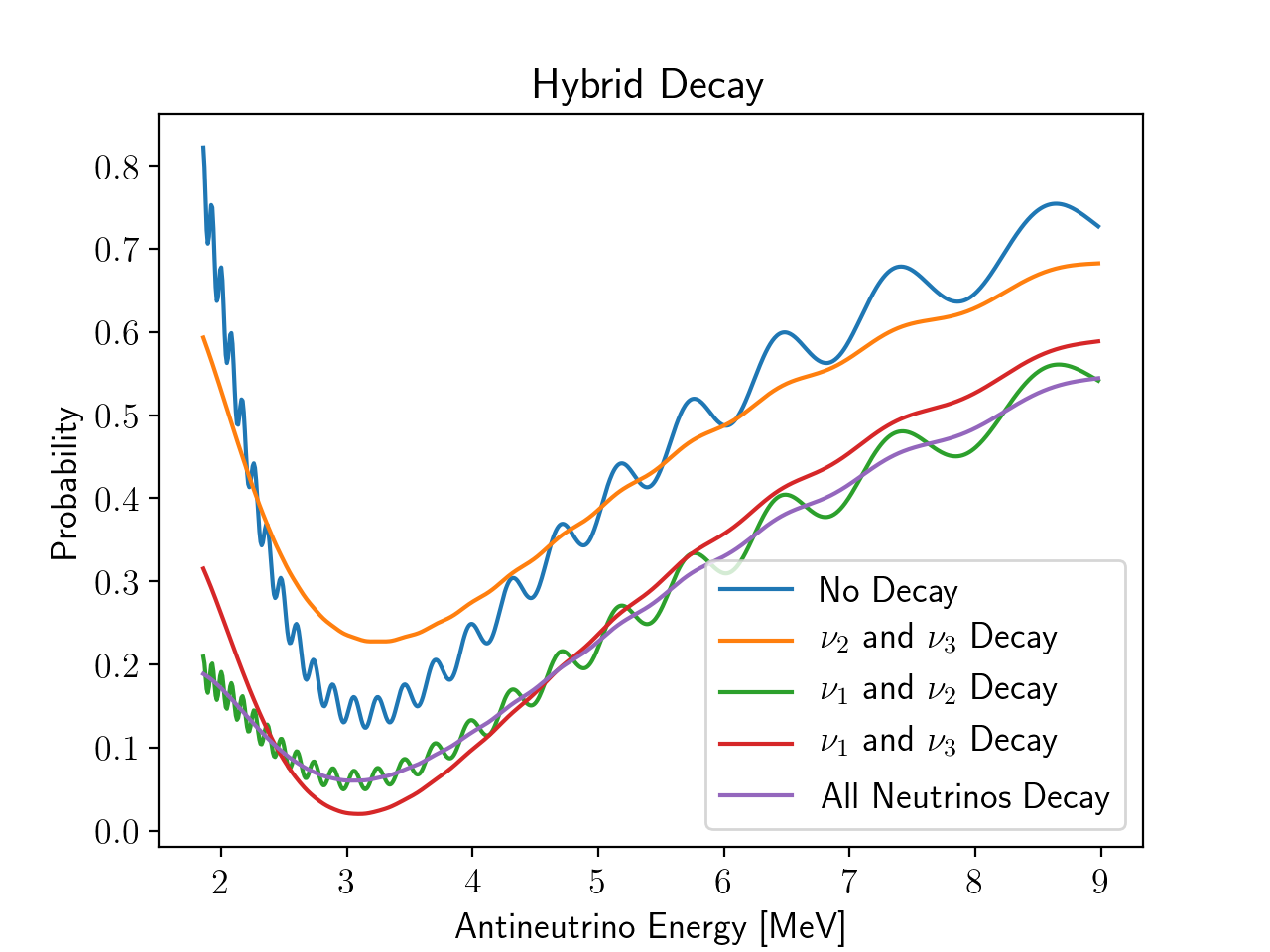
Results and Discussion
Once we demonstrated the effect of neutrino decay on the flavor oscillations, we determined reasonable bounds for the lifetimes of the
neutrinos. To set initial constraints on our lifetimes, we performed chi-square tests on the decay factors, which are related to the
lifetimes by miΓi = mi/τi where miΓi is the decay factor
for νi decay, and τi is the lifetime of νi. Using the 2σ statistic, we found our initial
upper bounds to be 7.39e-8 eV2, 2.50e-7 eV2, and 6.52e-6 eV2 for m1Γ1, m2Γ2, and
m3Γ3, respectively. Once we determined these initial bounds, we used two-dimensional chi-square tests to look
for correlations between the oscillation parameters and the decay factors, and we found that the strongest correlation exists between the
solar mixing angle and m1Γ1 and m2Γ2. There was also a correlation between m3Γ3
and sin2θ13, but we did not pursue this further as there already exists strong constraints on sin2θ13
from other experiments.
Once we found the correlation between the solar mixing angle and the decay factors, we further improved our estimation the upper bounds
on the decay factors using a reduced chi-square. We marginalized sin2θ12 and performed the reduced chi-square
tests on the decay factors. Our new upper bounds were determined to be 1.20e-7 eV2, 4.45e-7 eV2, and
6.67e-6 eV2 for m1Γ1, m2Γ2, and
m3Γ3, respectively. The original and reduced chi-square tests with the decay factors are shown below. As expected,
the reduced chi-square curves are shallower than the original, non-reduced chi-square curves.



Conclusions
We first concluded that ν3 decay suppresses the small neutrino oscillations, which are driven by Δm231 and sin2θ13, ν2 decay suppresses the long oscillations, which are driven by Δm221 and sin2θ12 , and ν1 decay roughly reduces the overall number of neutrino events. We then determined reasonable bounds on our decay factors and showed the correlation between the solar mixing angle and the decay factors using chi-square analysis. Lastly, we marginalized the solar mixing angle with the decay factors, which allowed us to improve our constraints on the decay factors. In the future, we anticipate our estimates can be tested by the JUNO experiment.
Acknowledgements
This material is based upon work supported by the National Science Foundation (NSF) under Grant Number 175779. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the NSF