FINDINGS

Symmetric Case of Two Species

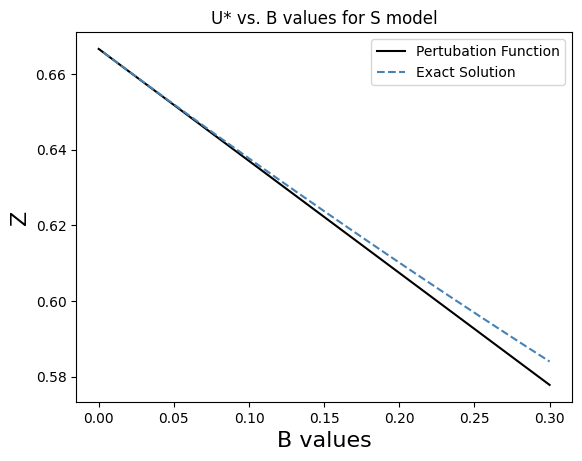
We include nonlinear crowding, with parameter, B, where 𝐵 > 0 and, for simplicity, we take 𝑟 = 1. For F and S communities, coexistence will be stable under the exact reverse of the stability conditions for the single- species case, i,e., when 𝛼 < 1 + 𝐵 for F , and 𝛼 < 1 − 𝐵 for 𝑆. When these conditions are satisfied both species reach a stable state 𝑢∗ over time, independent of initial conditions. The transition point where species shift from single-species dominance to coexistence is α = 1 + B for 𝐹 communities and 𝛼 = 1 − 𝐵 for 𝑆 communities. Our model of nonlinear crowding growth is controlled by 𝐵. When 𝐵 > 0 the terms in red now describe our model of nonlinear crowding. The crowding term can incorporate faster than linear growth (− sign in the red denominator - F community) or slower than linear growth (+ sign in the red denominator - S community). For simplicity we describe our results only for the symmetric case when β = α . When 𝐵 = 0 the classical result is that coexistence will be stable if 𝛼 < 1 while the single species states will be stable for 𝛼 > 1 (bistable regime). For 𝑆 communities the single-species states are stable if 𝛼 > 1 − 𝐵 while for 𝐹 communities the(window for coexistence, e.g., biodiversity, shrinks) single species states are stable if 𝛼 > 1 + 𝐵(window for coexistence, e.g., biodiversity). In the symmetrical case the coexistence point (𝑢∗, 𝑣∗) satisfies 𝑣∗ = 𝑢∗ where 𝑢∗ is a root of a quadratic equation. The two roots are:

$\displaystyle{u_{*} = -\frac{(1+\alpha-B) \pm \sqrt{(1+\alpha-B)^2+4(\alpha B)}}{2 \alpha B}}$

We have developed perturbation and asymptotic expansions for the roots for small 𝐵.

Asymmetric Case of Two Species

For the asymmetric case, we take 𝛼 ≠ 𝛽 and the equations are in the form outlined in the symmetric case. For 𝐹 communities, we showed that for the 𝑏10 (𝑢 wins, 𝑣 loses) state to be stable, the parameters must satisfy 𝛽 > 1 + 𝐵. Similarly, for the 𝑏01 (𝑣 wins, 𝑢 loses) state to be stable, the parameters must satisfy 𝛼 > 1 + 𝐵. Similarly, for 𝑆 communities, the transition point for the 𝑏01 state is 𝛽 = 1 + 𝐵 and for the 𝑏10 state 𝛽 = 1 − 𝐵 . The coexistence state for the asymmetric case (𝑢∗, 𝑣∗) satisfies the coupled quadratic equations which cannot be solved explicitly. As an example, for 𝐹 communities the system is:

$\displaystyle{0=1- (\beta+1)u_{*}-\alpha v_{*} +B \alpha u_{*}v_{*}}$

$\displaystyle{0=1-(\beta+1)v_{*}-\beta u_{*} +B\beta u_{*}v_{*}}$

We have demonstrated coexistence 𝐵 is small, but due to the complicated nature of the coupled equations, we have not been able to analytically determine transition values when crowding growth is nonlinear.

Symmetric Case of Three Species

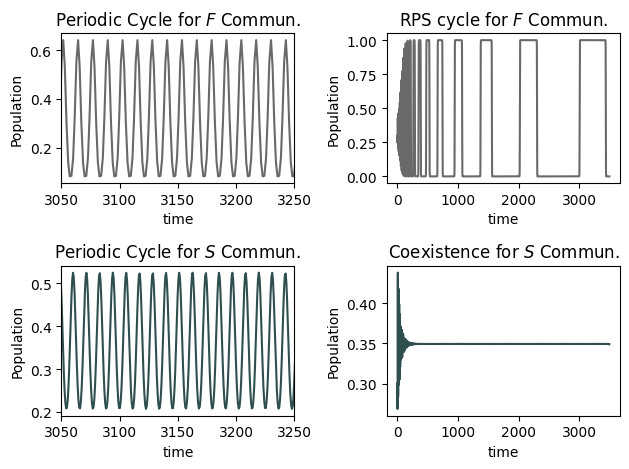
We next studied a three-species cyclic system. Such systems are often referred to as rock-paper-scissors (𝑅𝑃𝑆) system because of the clear analogy with the classical children’s game, Bayliss et al. (2019). After appropriate non- dimensionalization and assuming that all natural birthrates are equal, the system of ODEs governing this ecological system takes the following form:

We next considered the impact of the nonlinear crowding effect ($B>0$) and considered both faster and slower than linear growth communities ($F$ and $S$ communities, respectively). We took $B = 0.1\,$. For specific ranges of $\alpha$, the interval $[2.1,2.2]$ for $F$ communities and [1.60,1.8] for S communities), a new behavior emerges - a window of periodic solutions, describing a periodic change in dominance for the system. In this scenario, each species dominates the ecosystem for a specific duration, and as time approaches infinity, the time intervals for each species’ dominance remain constant. This periodic window is not observed for linear crowding ($B=0$).