Abstract
Neutrinos oscillate between different flavors as they propagate.
Neutrinos have 3 flavor states and 3 mass states. Each flavor state \(\lvert \nu_\alpha \rangle \) can be written in terms of the 3 mass states \(\lvert \nu_i \rangle \),
\(\lvert \nu_\alpha \rangle = \sum_i U_{\alpha i} \lvert \nu_i \rangle \),
where \(\alpha = e, \mu, \tau \) and \(i = 1, 2, 3 \). The matrix \(U\) is unitary and is at the center of the traditional neutrino propagation model.
Current and future experiments that measure neutrino oscillations can be modeled.
\(\bar{P}_{\alpha \beta} = \left( \int_{E_i}^{E_f} dE \frac{d\Phi}{dE} \sigma(E) P_{\alpha \beta}(E) \right) \Big / \left(\int_{E_i}^{E_f} dE \frac{d\Phi}{dE} \sigma(E) \right)\)
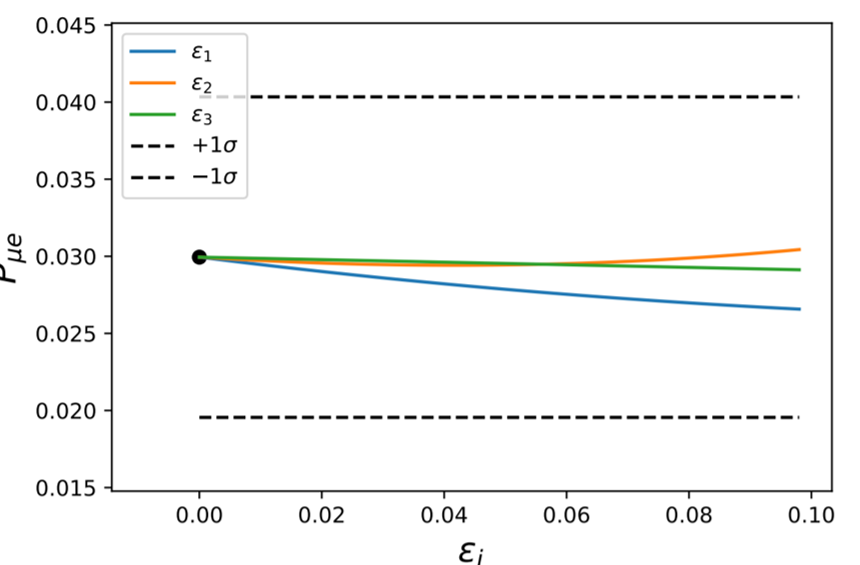
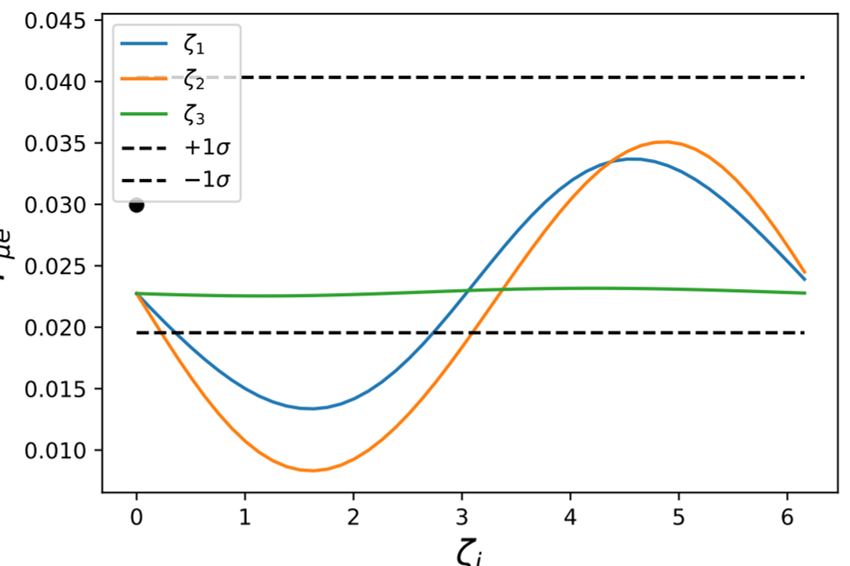
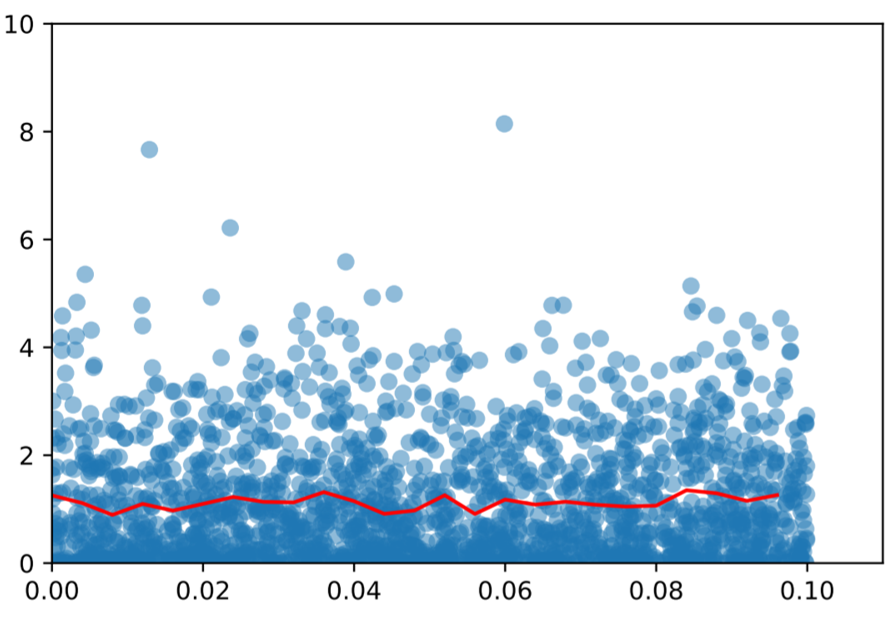
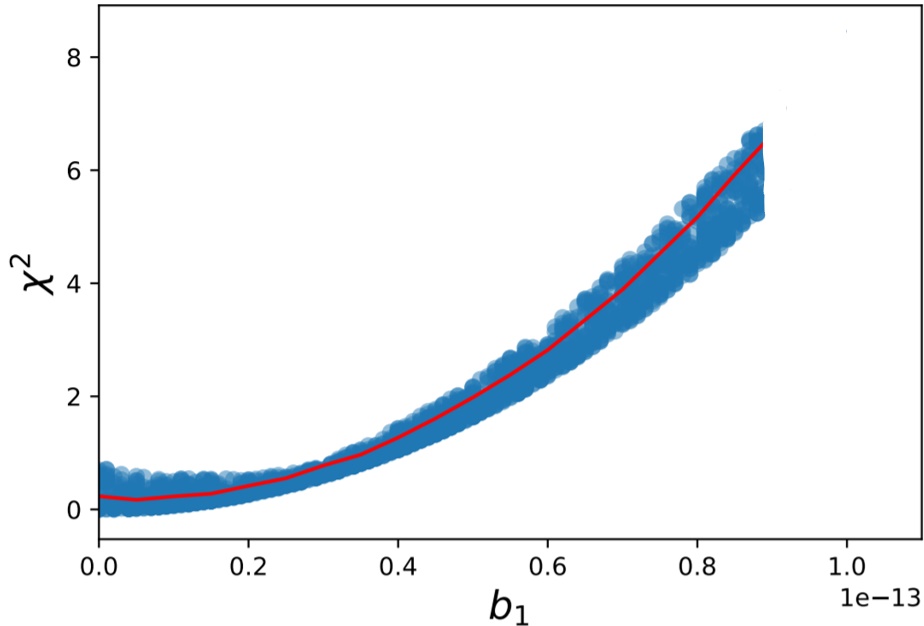
The average transition probability \(\bar{P}_{\alpha \beta}\) from flavor \(\alpha\) to \(\beta\) is modeled by calculating the fraction of detected neutrinos with oscillations over that without oscillations.
Two experiments that can model these oscillations are Tokai-to-Kamioka (T2K) and the Jiangmen Underground Neutrino Observatory (JUNO)
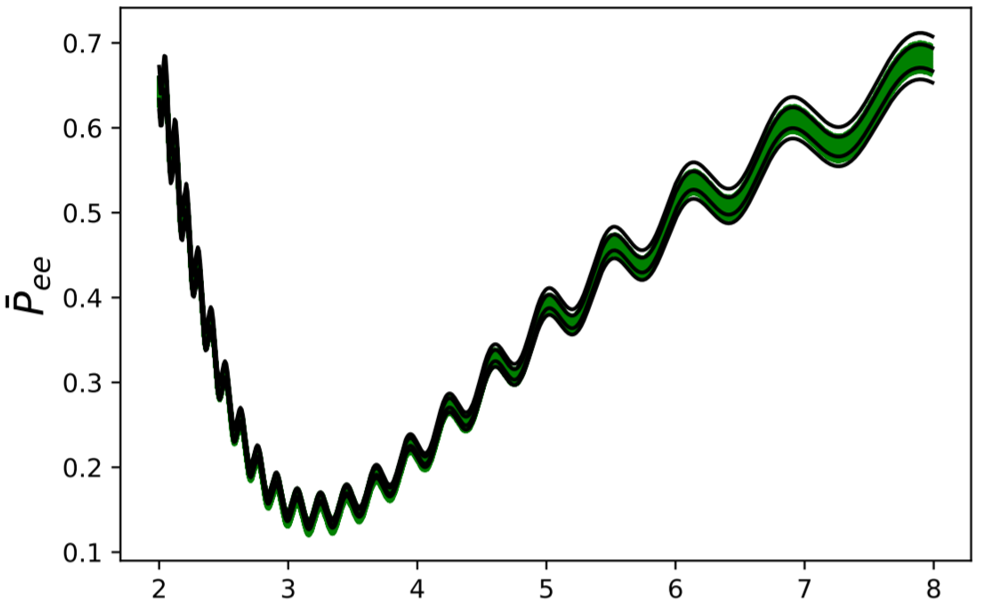
The T2K experiment measures the average \(\mu\)-to-\(e\) neutrino oscillations over the entire energy spectrum of incoming neutrinos. JUNO is expected to measure electron neutrino survival (\(e\)-to-\(e\)) probabilities over a range of energies.
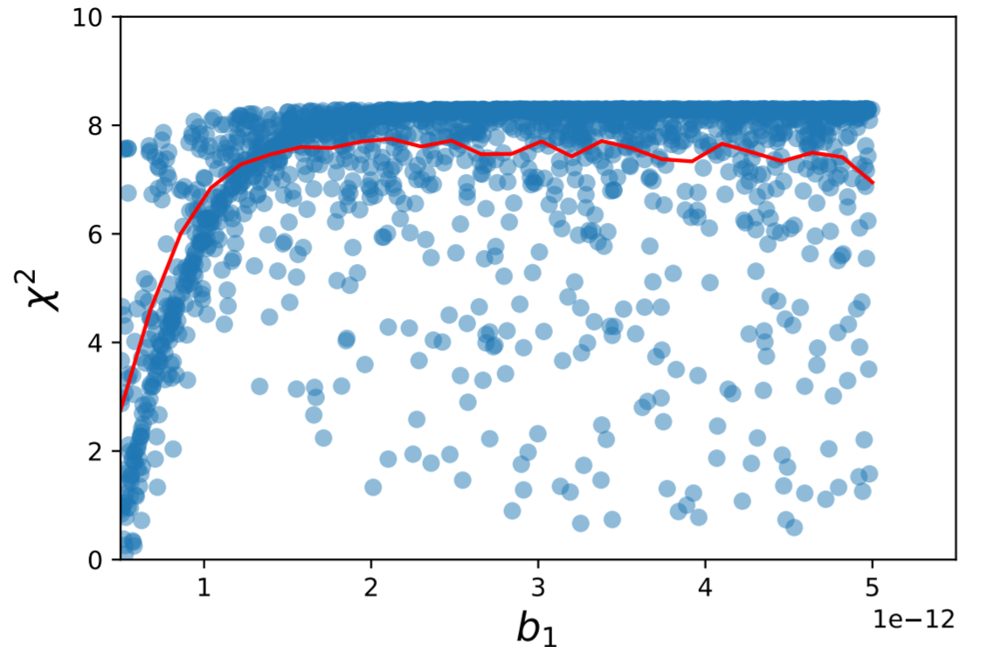
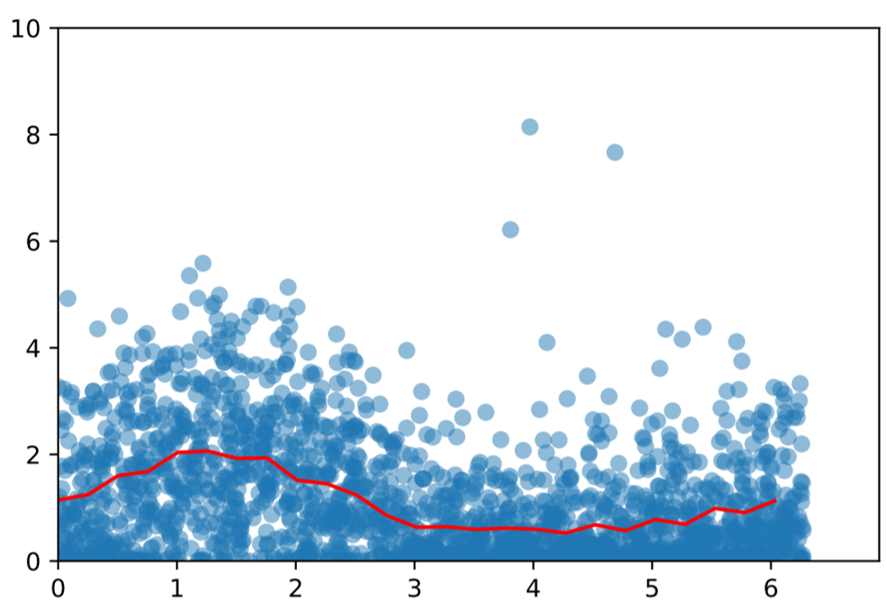
The expected number of detection events (flux times cross section) was estimated using the curves provided by the T2K [1] and JUNO [2] collaborations. The baseline distances for neutrino travel are 295 km (T2K) and 53 km (JUNO).