Introduction

The Vulcanoids are a population of suspected asteroids that are predicted to be located between the Sun and Mercury at distances of 0.05-0.25 AU. The Vulcanoids are of interest because they would have formed during the early years of the Solar System, and they would give specifics about the history of the Solar System. Leftover planetesimals from the inner edge of the protoplanetary disk may also help explain why Mercury has a significantly smaller mass than the other terrestrial planets, and also why seventy five percent of the planet is composed of metal Rubincam (2000). Searches for the Vulcanoids have been carried out such as Campins (1996), who tried using near infrared arrays at the Kitt Peak National Observatory in efforts to discover the Vulcanoids, but the search was unsuccessful in finding any trace of them. Despite many attempted searches for the Vulcanoids, none so far have been found and thus the question of why still stands. This paper is intended to explain why the attempted searches have failed, and demonstrate what happened to the Vulcanoids.

The YORP Effect

The YORP (Yarkovsky O'Keefe Radzievskii Paddack) Effect has the ability to spin up/down bodies that are close to the sun, which heavily applies to the region suspected to contain the Vulcanoids. The YORP effect is driven by incoming photons from the sun which hit the surface of the asteroid. As these photons are reflected from the surface, a small torque is applied to the asteroid due to the small amount of momentum that photons carry Rubincam (2000). This torque is dependent on the geometry of the asteroid, so in order for spin up/down to be achieved, the asteroid must be non-spherical in order to be affected by a net torque i.e cause the asteroid to rotate. This process is slow in nature, so only after a long period of time is it possible to have alterations in the rotation rate of the asteroid. The YORP Effect is also dependent on the radius of the asteroid, meaning bodies with smaller radii r>10km will spin up/down at a faster rate than bodies with radii larger than 10km. The YORP effect can also be applied to larger bodies, r>10km, that are within the prospective region for Vulcanoids, to also explain why larger possible Vulcanoids haven't been discovered.

The YORP Time

The YORP time is used to describe how long it takes for an asteroid to go through a cycle of spin up/down due to the YORP effect. The Yorp time is also heavily dependent upon the size and shape of the asteroid, but also the distance from the sun and eccentricity of the orbit will also change the YORP time. Bodies that are smaller in radii and closer to the sun will experience larger effects of the YORP and thus a shorter YORP Time. Bodies that are farther away from the sun and larger in radii will result in decreased effects of the YORP and a longer YORP time. Because the predicted region for the Vulcanoids is close to the sun, larger bodies R>10km that would not be candidates for the YORP effect are modeled to show successful effects of the YORP, and thus have YORP times that are short enough to explain why larger Vulcanoids haven't been discovered as well. The YORP coefficient is determined by the shape of the asteroid, such that when Y>0, this entails that the asteroid will be able to spin up to the critical disruption frequency omega_d (Jacobson 2014). Because the YORP time is shape dependent asteroids that are asymmetrical are prime candidates for the YORP effect. Asteroids that are more asymmetric will experience a higher net torque causing the spin up/down versus an asteroid that is close to being spherical.

Results

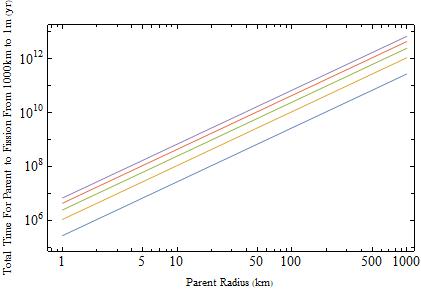
In order to describe how a parent asteroid breaks into its subsequent gennerations, a YORP time scale specifically for the parent Vulcanoid had to be developed. t_0 is the Parent YORP time (also referred to as the Initial YORP time). This timescale defines the duration of an YORP cycle (Steckloff 2015). Because the children asteroids will have radii smaller than those of the parent this will result in a shorter YORP time, and will require less time for the new generation asteroids to spin up to critical disruption velocity. The radius of the child asteroid is only a fraction of the parent asteroid radius (Steckloff 2015). Using the ratio of radii between the parent asteriod and child, and also factoring in the shorter YPRP time taken by each new generation, the total time taken for a parent of radius R to fission down to radius r can then be calculated. Further assumptions on how the parent breaks apart and the effects on the total timescale are currently being worked on, and will be included at a later time.