Spring 2013: Visualizing String Drifferences and the Linguistica Project







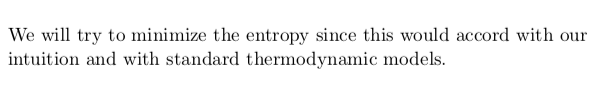




General Thoughts on Linguistics
I think that with few exceptions any respectable scientist since the time of William of Ockham would say that a scientific theory should be simple and elegant. I will refer to this widely accepted belief as the Postulate of Theoretical Parsimony (or PTP). It will be helpful to begin our discussion with three quotes. The first is from Doctus Ockham: “When you have two competing theories that make exactly the same predictions, the simpler one is the better.” (Note that this is probably not a translation faithful to the actual words of Ockham so much as the spirit of what he meant.)The second quote is from Paul Adrien Maurice Dirac who was a physicist who did seminal work on quantum theory and laid the foundations of quantum field theories, particularly of quantum electrodynamics. He claimed that: "God used beautiful mathematics in creating the world."
The third quote is from Ray Solomonoff who developed the theory of universal inductive inference. He argued that: "The strongest evidence that we can obtain for the validity of a proposed induction method, it that it yields results that are in accord with intuitive evaluations in many different kinds of situations in which we have strong intuitive ideas."
I hope that these quotes hope to highlight the important roles that the notions of simplicity and elegance have in the practice of science. More importantly I hope that they draw attention to the fact that scientists have certain biases that they follow in constructing theories. For Ockham it would be a philosophical and religious desire for simplicity, for Dirac a certain aesthetic notion that the right theory is alluring in some mathematical sense, and for Solomonoff it would be the desire to keep theory intuitive. The biases, commitments, ideological stances, and personal loyalties that scientists have is fascinating and provides deep insight into the nature of science and how it is practiced.
As I see it, the questions thus far for which the working linguist is trying to provide answers to are the following: 1. Does the status of Linguistics as a science depend on its coverage of psychological and neurological issues? 2. What makes Linguistics a science? 3. What is the nature of Linguistics empiricism? 4. Are Minimum Description Length models a good framework for linguistic theorizing? 5. Does the linguistic analysis that is plausible based on language data still plausible when the realities of neural computations, the few we are sure of, are taken into account? 6. What are the theoretical primitives on which Linguistics should be built up from?
By way of summary, I have claimed that the answer to (1) is a definite NO, although the questions of psycholinguistics are very important, and neurolinguistics might one day provide great insight into the search space problem in Linguistics if certain linking hypotheses on which the field is based are either proven or replaced with something more analytically tractable. Regarding (2), I have suggested that Linguistics is a science by dint of its attempt to explain language data from experiments or fieldwork on the basis of the theoretical commitments outlined in my maiden blog post.
I see questions (3) and (4) as being very intimately related in that the empirical method of Linguistics can be cast in terms of maximizing the probability of the data under study while at the same time expressing generalizations regarding the regularities in the data in as economical a way possible without providing trivial insight. Minimum Description Length models provide powerful mathematical tools in order to formalize this method. I hope that using such methods will one day provide a principled basis on which to do linguistic theory when considered alongside insights from other theoretical orientations. (5) and (6) are very much open ended questions and I feel that my opinions about them change all the time.
So....How then do answers to these questions have anything to do with simplicity and elegance? They are principles relevant to linguistic work because a good linguist holds dear the Solid Ground Commitment (the commitment to use theoretical tools that are well understood to develop a non-ad hoc explanation of a phenomenon) and the PTP regardless of other commitments they might hold. Moreover, the PTP in large part informs a linguist's choice of theoretical tools (.......as well as other sociological and pragmatic concerns).
But more importantly the desire for simplicity has almost become pathological in modern theoretical linguistics as various researchers use it as the justification for the advancement of a new theory or for the revision of an existing one. If notions of simplicity and elegance are not to become meaningless banners raised in the name of serious scholarship we must assign them definitions which accord with our intuitions about how they ought to be used in the practice of science.
But that's the sticking point.
There is little agreement in any science, whether physical or social, on what simplicity and elegance mean in the context of scientific investigations. A theory which might be simple and elegant for one researcher might be convoluted and stilted to another. In this way, it is easier to talk about competing notions of the PTP rather than to claim the existence of a monolithic one. Some competing variants of the PTP that I have observed in practice are: the Biological PTP, the Cognitive PTP (about which I have talked a little), the Mathematical PTP, and the Emergent PTP. I will talk about these PTP variants in the context of Linguistics, but I think there are analogs for them in each of the sciences.
The Biological PTP is mostly invoked in the social sciences and Biology and is roughly equivalent to the claim that a theory must provide explanations that explain why something would occur based on evolutionary and genetic principles. The invocation of this PTP variant in Linguistics particularly distresses me in that it leads to some assuredly bizarre justifications for "developments" (yea, those were scare quotes) in Minimalist syntax and other branches of Linguistics. Take for an example a recent discussion about the faculty of language (FOL) by a certain well known GGer who claims that a GG with simple generative mechanisms is to be favored because of the evolutionary pressures on early humans that first developed the use of FOL.
That is, this linguist is claiming that the synchronic GG of the speakers of modern languages must be based on conceptually simple systems "given what our ancestors had available cognitively about 100k years ago" [original italics]. I think it is clear that no one knows what our ancestors had available cognitively about a 100 thousand years ago so as far as I am concerned such considerations must not factor into a theory of language. This is not to say that Darwin's Problem (the problem concerning how the language capacity developed in our species) is unimportant. I think it is important but ultimately perhaps not amenable to analysis without more direct evidence of the linguistic abilities of our ancestors. Although I think people who work in computational learning theory of formal languages would answer this question in a different way and I would mostly agree with them. They would say that we should determine the smallest class of languages to which human languages belong (probably a slight modification of the Mildly Context Sensitive Languages) and then attempt to see whether that class is learnable using an efficient and fast algorithm that would explain data from psycholinguistic experiments with children acquiring their first language. We will talk about this more later when we talk about the Mathematical PTP.
The Cognitive PTP has some overlap with the Biological PTP in a limited way; it says that a simple and elegant theory must explain phenomena using the tools of psychology and neuroscience preferably with representations that are the same as those believed to be used in the actual brain. (The overlap comes from those researchers who work in evolutionary psychology.) I will limit my comments here because I have talked about this issue in my previous blog. I think it is important to note that people who hold dear the Cognitive PTP have to accept that we do not know that many definite things about the brain even given our ability to plumb its inner workings with gross dissection, MRI, PET, brain lesion studies, and the like.
Particularly, we do know a fair deal about neuroanatomy and how the brain is connected structurally but we do not know how the brain computes the mind as a physical system. So for those researchers that subscribe to the view that the study of the mind is the same as the study of the brain the next few years are going to be rough as they come to accept the difficulty of the Black Box problem in neuroscience. If you think this isn't the case, I beg you to consider the strange case of Caenorhabditis elegans-the nematode. As I have been told by a professor, the complete nervous system of the nematode has been mapped but it is still mostly a mystery how it is able to wiggle its backside or to make a decision to move.
The nervous system of human beings is much, much more complicated than that of our friend the nematode so it would be pure folly to think that at present we could be capable of understanding the human nervous system if we are unable to understand the nematode's. In terms of David Marr's levels of analysis, it would be safe to say that researchers are stuck working at the physical level and computational level, and I think it is safe to say it will be a little longer before we understand the algorithms or representations that the brain actually employs. {For reference, and I take this from Wikipedia, Marr's levels of analysis in neuroscience are the following: computational level: what does the system do (e.g.: what problems does it solve or overcome) and similarly, why does it do these things algorithmic/representational level: how does the system do what it does, specifically, what representations does it use and what processes does it employ to build and manipulate the representations physical level: how is the system physically realized (in the case of biological vision, what neural structures and neuronal activities implement the visual system)}
The Mathematical PTP says that a simple and elegant theory is one that is expressed in a logical mathematical formalism with appropriate axioms and theoretical primitives. People who hold dear there mathematical PTP are predominantly formalists and a good part of them rank the Formal Symbol System Commitment ("the commitment to the central Chomskyan metaphor, namely, that a language is a formal symbol system") as their highest theoretical priority. I think the work done in this vein of Linguistics is important (look at work by Edward Stabler and colleagues, Aravind Joshi, Alexander Clark, Emily Bender among others) and that the mathematical tools of Formal Language theory, the Theory of Computation, and Computational Learning theory have the potential to provide new insight in Linguistics, but I fear that, at times, some of the formal accounts of language data are mere abstract symbol manipulation. I find this to be most true of work in some branches of Formal Semantics, but I admit that this is just unfair skepticism based on my desire for a theory of meaning to be grounded in Lexical Semantics.
The Emergent PTP is similar to the Mathematical PTP in that it stresses the importance of having theory be based on non-adhoc principles, but it differs in that it says that a simple and elegant theory is one that grounds its explanations in natural law. On this view, a good theory would be one that starts with the principles of Physics and arrives at a theory of Language, so the human language faculty follows from physical principles. This seems to be a view that Chomsky is championing in his recent work on Minimalist theories by arguing that simple generative mechanisms are to be preferred because physical systems tend to behave optimally. Whether this is true or not, I do not know, but I think everyone will agree that working from first principles is to be desired whenever possible.
What then are we to make of these PTP variants? Are they simply different, but equivalent, theoretical orientations from which to work or, are they conflicting viewpoints whose results will need to be resolved in some way? I am not sure that I have an answer to that question, but I favor a formal approach that is capable of expressing the full complexity of linguistic data and generating the intuitive results that we would require of a theory of language. I would cast my vote for the Mathematical PTP, if I were to choose one theoretical stance from which to work, but I understand that the more interesting work in Linguistic is one that integrates work from multiple different theoretical viewpoints. Importantly, such a view does not sustain the claim that all viewpoints are created equal, and the determination of which theoretical perspectives are unequal is ultimately based on the opinions of individual researchers.