Summer 2019: Work with Dr. Dahl on the Scintillating Bubble Chamber (SBC) Experiment at CIERA

Abstract of Project

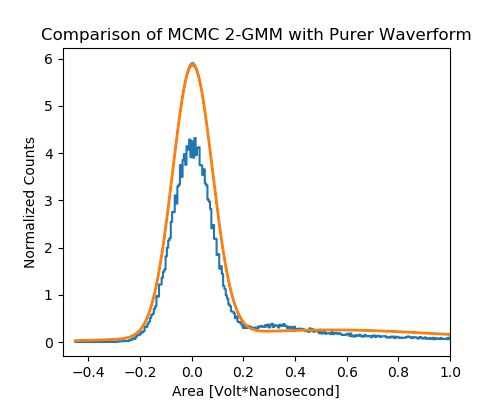
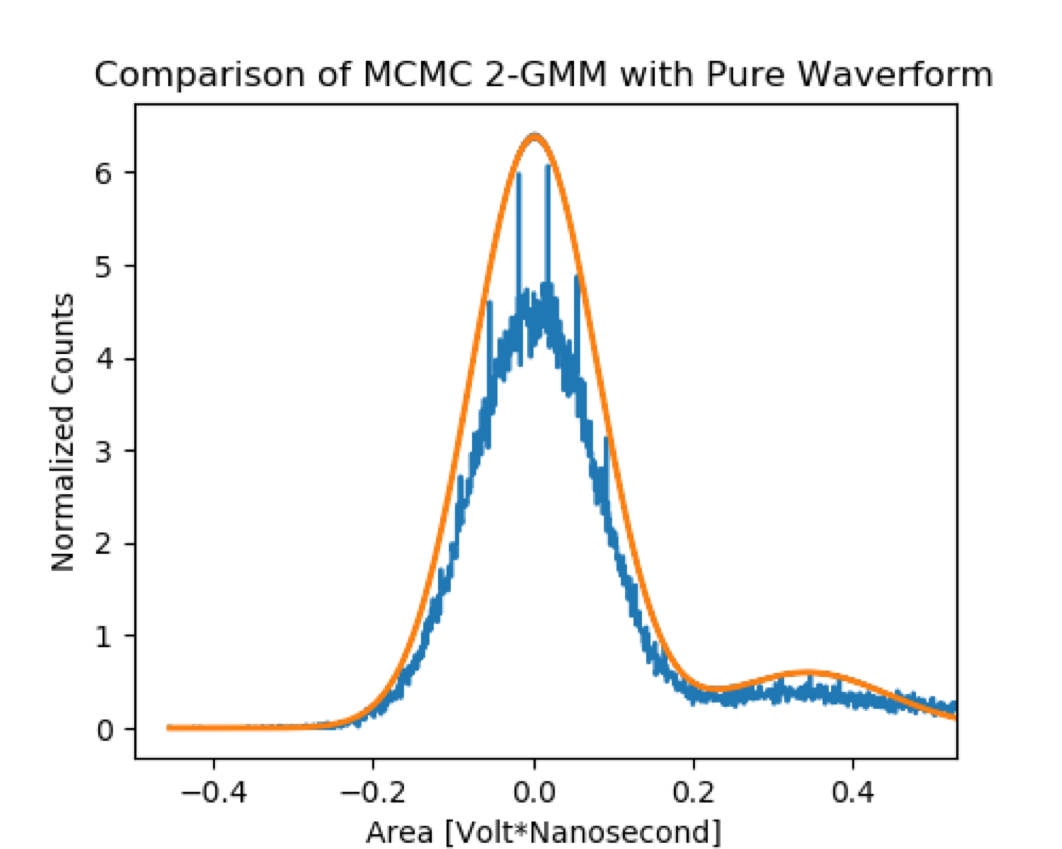
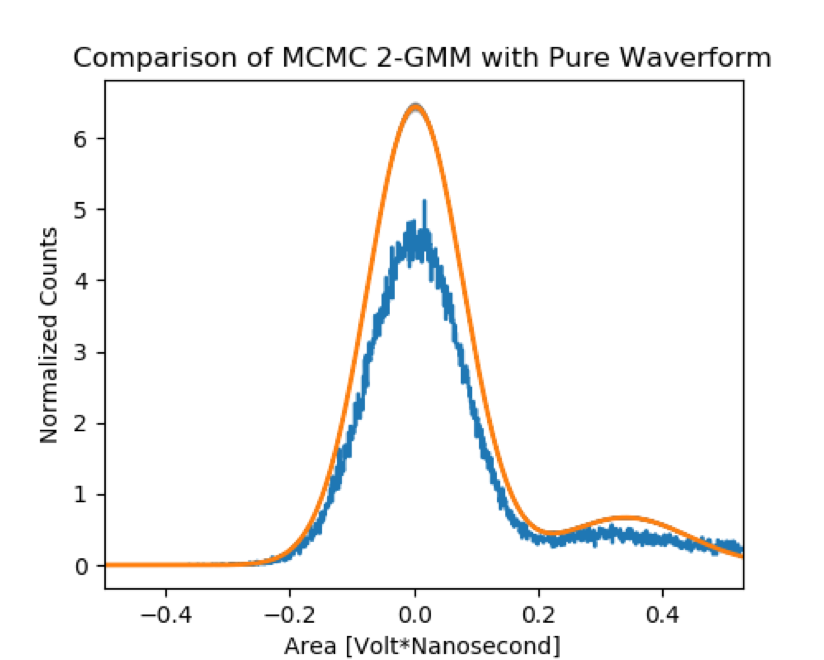
It is believed today that most of the matter in the universe is not composed of Standard Model Particles, but rather of Dark Matter (DM). DM is thought to constitute 85 percent of the matter in the universe. Direct detection of DM is extremely difficult for a myriad of reasons, but bubble chambers have proven to be good experimental probes of the parameter space that DM is suspected to reside in. The Scintillating Liquid Argon Bubble Chamber (SBC) is a novel experiment that couples the advantages of bubble chambers with the production of scintillation light for each DM candidate particle. The scintillation light in the SBC experiment is used to measure the energy deposited by the DM particle. The scintillation light is captured by silicon photomultipliers (SiPMs), which are solid state light detectors capable of single photon detection. This detection is performed by incoming photons being converted into charge at the p-n junctions in the diodes of the SiPMs. The converted photoelectrons are amplified to a detectable current by a cascade effect within the SiPMs, and the proportionality factor of the amplification is ideally linear and is called the gain. Gain is one of the significant sensitivity parameters that characterize a light detector, and in the context of the SBC experiment the calculation of the gain for SiPMs is especially important because it is used to determine energy left by possible DM candidate particles. In the present work, a novel technique for calculating the gain is explored that employs emcee, an open source Python implementation of the affine-invariant ensemble sampler for Markov chain Monte Carlo (MCMC) proposed by Goodman (2010). Fig. 8 shows that the chosen model is in bad agreement with the data in that it overestimates the gain and its uncertainty. The model used in the fitting procedure did not account for the effects from the truncated interval, and therefore the fit could be improved by using a truncated Gaussian. This is an area for further work as well as exploring the effect of different filters on the signal to noise ratios of the final version of the fitting procedure after the appropriate model is selected.

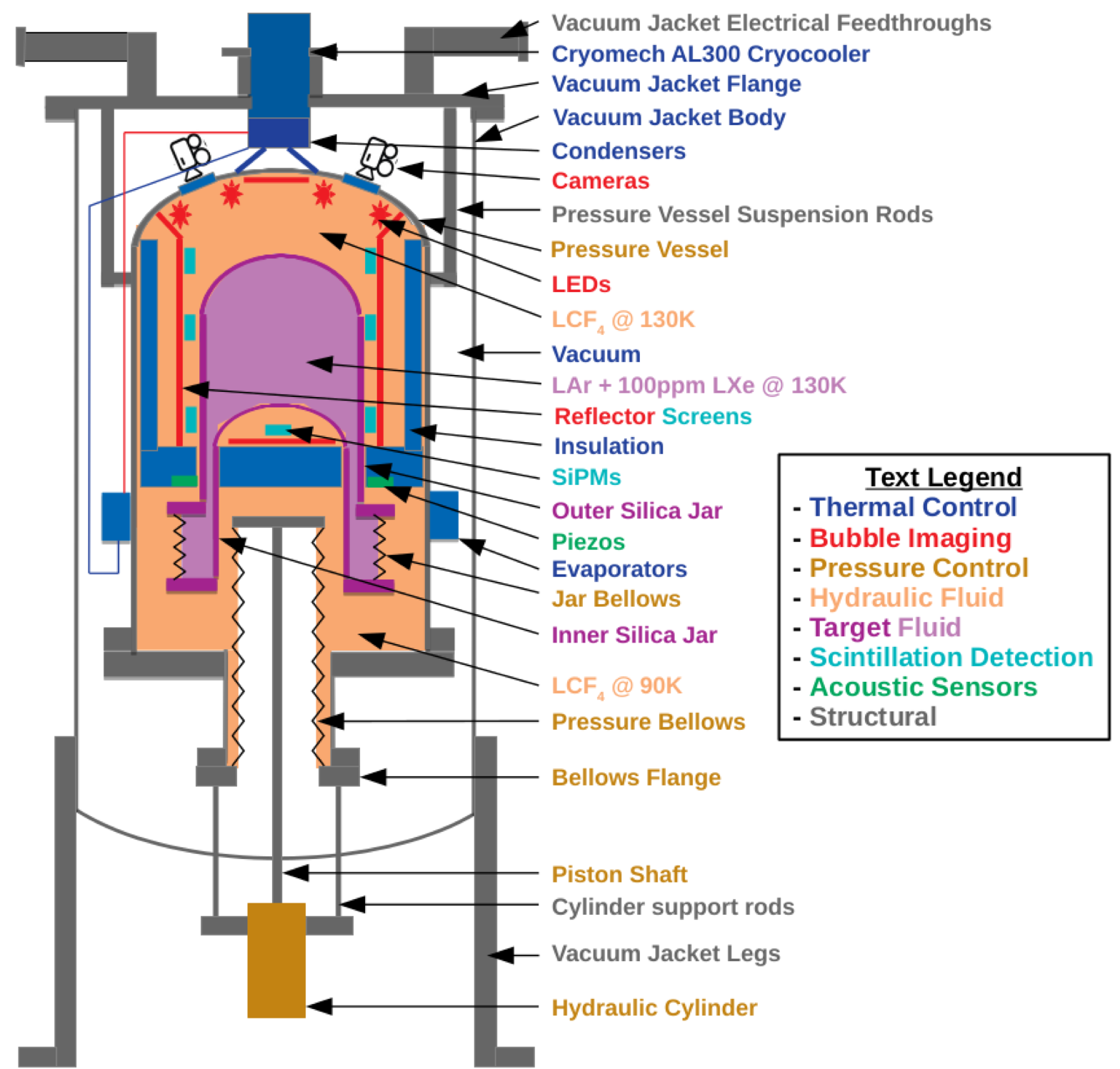
The Scintilating Liquid Argon Bubble Chamber (SBC)

Fig. 1:The chamber of the SBC is illuminated by IR LEDs so that cameras can detect and image the bubbles in the chamber. The piezoacoustic sensors hear the bubble nucleations and help to discriminate dark events. The VUV SiPMs capture the scintillation light produced by candidate particles and is used to measure the energy of a dark matter particle. Since bubbles and scintillation light cannot be looked for at the time, the piezos are needed in orderd to tie the measurements together.

Dark Matter and the SBC Experiment

It is believed today that most of the matter in the universe is not composed of Standard Model (SM) Particles, but rather of Dark Matter (DM). DM is thought to constitute ~85% of the matter in the universe. DM is inferred to exist because of its effect on galactic rotation curves among other reasons. DM can be produced at accelerators, detected indirectly with telescopes, or directly detected with ground-based experiments. Direct detection of DM is extremely difficult for a myriad of reasons, but the main two reasons for this are that DM candidates have a low probability of interacting with standard model particles, and there are many background sources that can be confused with a DM signal. Therefore, the design of a DM detector by direct detection necessitates minimizing sources of background, increasing the probability of DM interactions with the detector material, and discriminating DM events from background events.

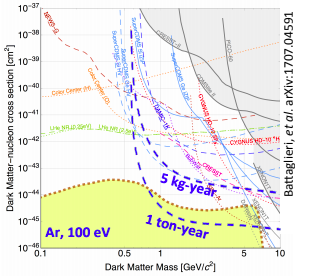
One kind of detector with these features is a bubble chamber. Bubble chambers are chambers of superheated fluid that produce a bubble when candidate particle interacts with the fluid. The Scintillating Liquid Argon Bubble Chamber (SBC) is a new detector currently being built by the SBC Group. The SBC can detect DM candidates above 0.5 GeV with sensitivity down to the solar neutrino floor.

Fig. 2:The blue curves show the regions that SBC will be able to probe for dark matter. The other curves are regions that have been ruled out by other experiments.

The innovative feature of the SBC is that not only does it produce bubble nucleation, but that it also produces scintillation light with each bubble. The production of a bubble excludes background events, and the scintillation light allows the energy of the dark matter particle to be measured. This precise measurement of a candidate particle’s energy makes the SBC a promising experimenting for detecting dark matter. The scintillation light in the experiment is captured by silicon photomultipliers (SiPMs). This research note details some of the preliminary work of work being done to characterize the sensitivity parameters of these SiPMs as well as their intrinsic noise. SiPMs are solid-state light-detectors that operate on the principle that certain p-n junctions in a diode will produce a current when struck by a photon. The amount of charge produced is proportional to the number of incoming photons. Ideally, the proportionality is linear and the constant of proportionality is called the gain. Gain is one of the significant sensitivity parameters that characterize a light detector, and in the context of the SBC experiment the calculation of the gain for SiPMs is especially important because it is used to determine the energy of possible DM candidate particles.

Characterization of Silicon Photomultipliers (SiPMs) for SBC Experiment

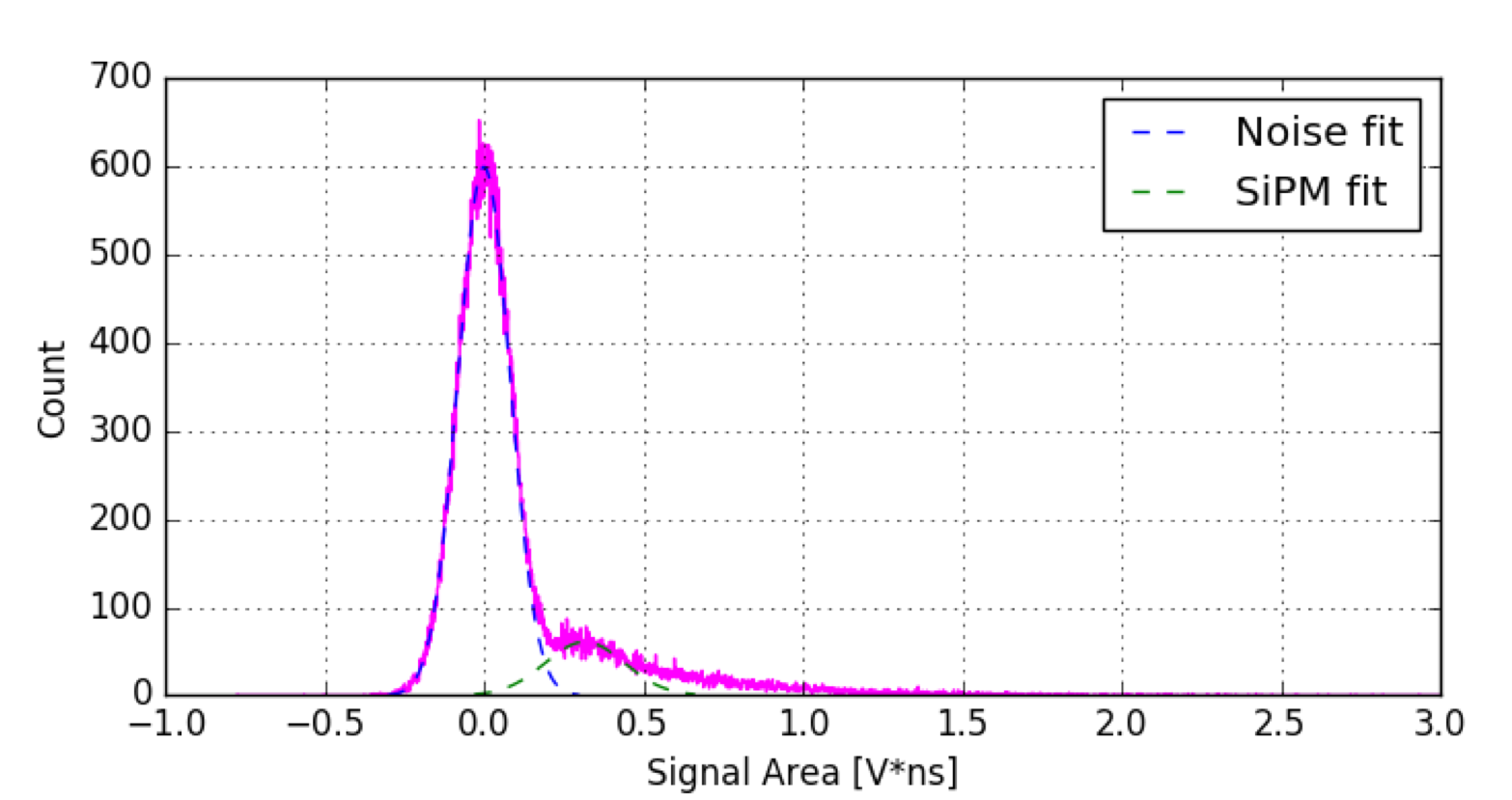
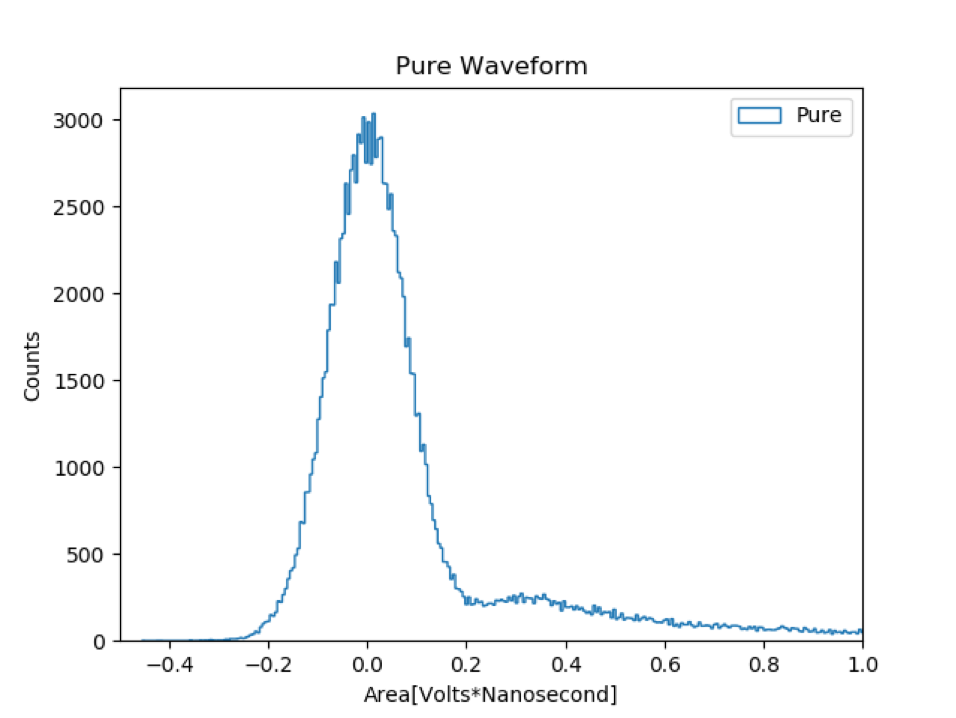
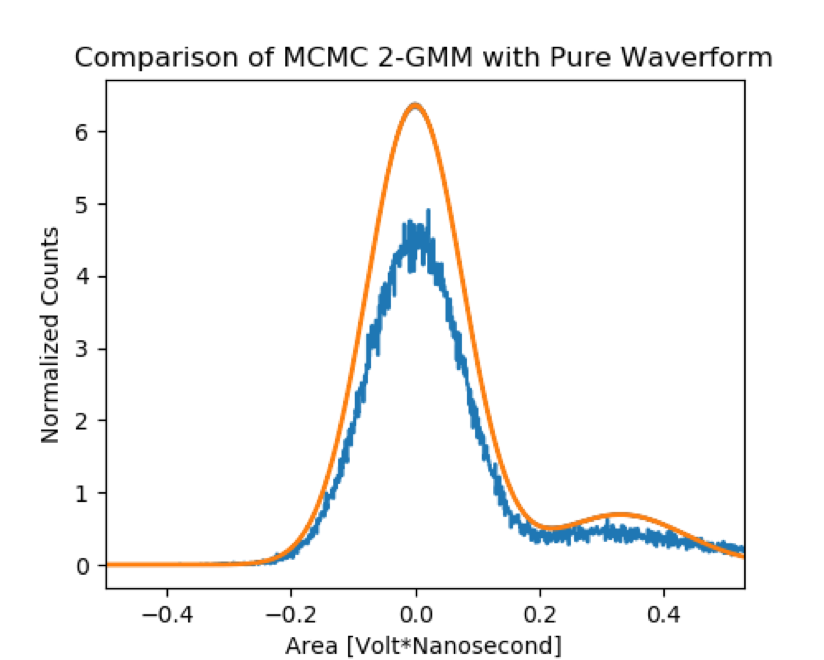
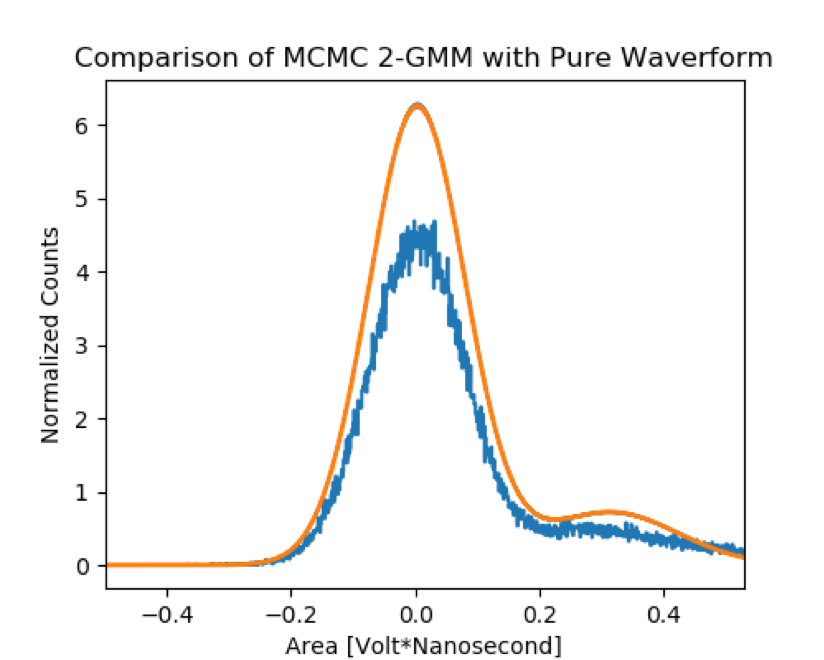
In the current SBC analysis, the gain is calculated by first integrating the digitized signal in variable time bins and turning that integrated signal into a histogram. The resulting histogram is bimodal with two peaks in which the peak centered around zero is due to electronic noise and the other is the single photon peak. The mean and variance of the singe peak are proportional to the gain and its uncertainty.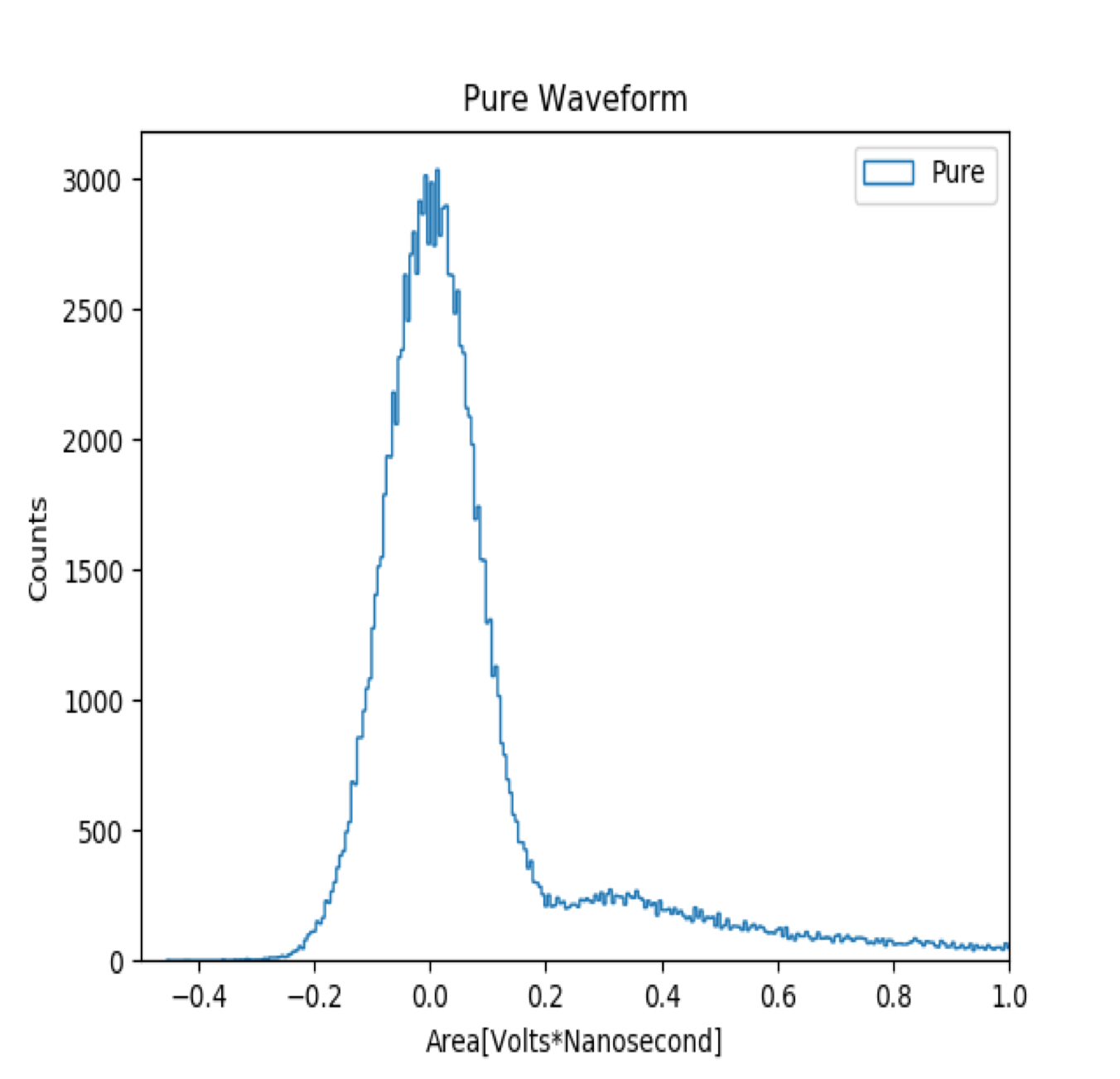
Fig. 3:Figure of the pure wave form produced by the current SBC analysis. The first peak is the noise peak, and the second peak is the single photon peak.

A previous group member calculated the mean and variance of the single photon peak by finding the local minimum between the noise peak and single photon peak and by then fitting two Gaussians between the local minimum, and max noise peak and max single photon peak.

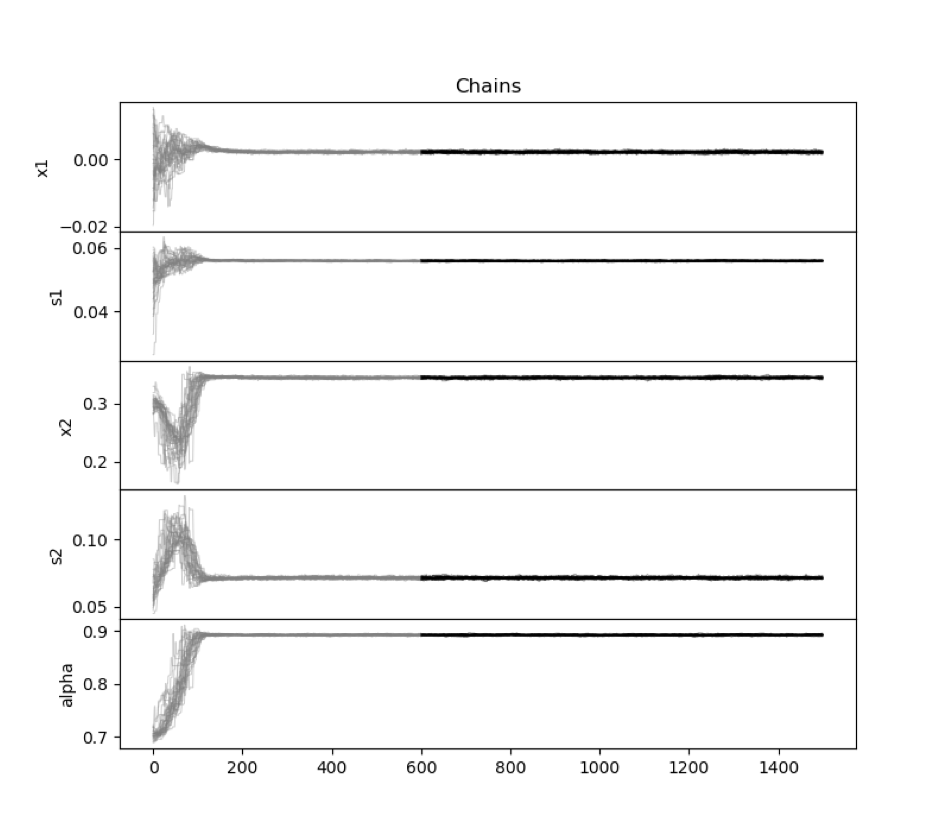
Fig. 4:Figure of the fit from previous group member's analysis compared with pure waveform.

This approach has the major drawbacks of being ad hoc and of overfitting the data. In the present work, we attempt to calculate the gain in a different way that avoids these shortcomings. The technique for calculating the gain is one that employs emcee, an open source stable, well tested Python implementation of the affine-invariant ensemble sampler for Markov chain Monte Carlo (MCMC) proposed by Goodman(2010).

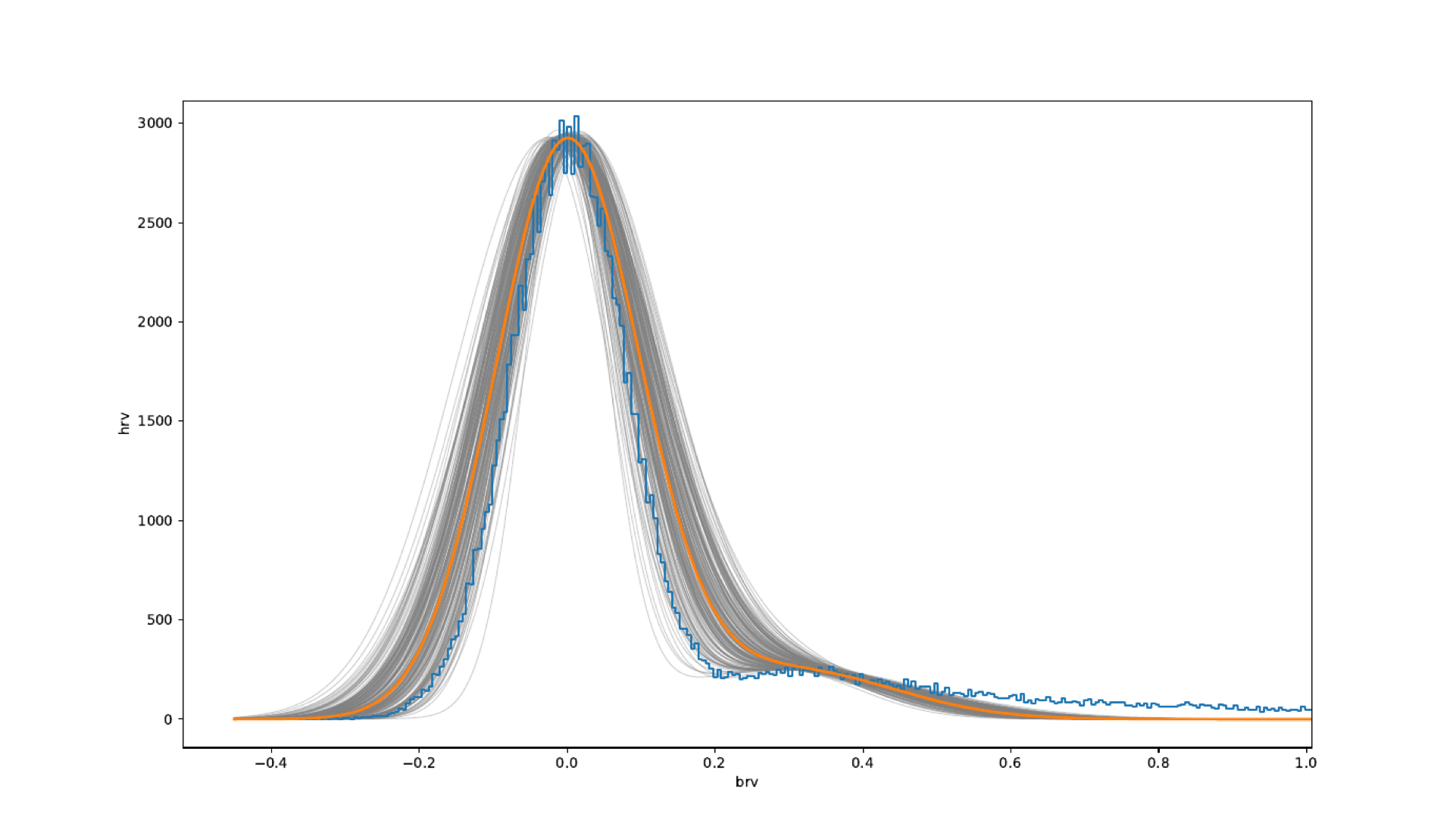
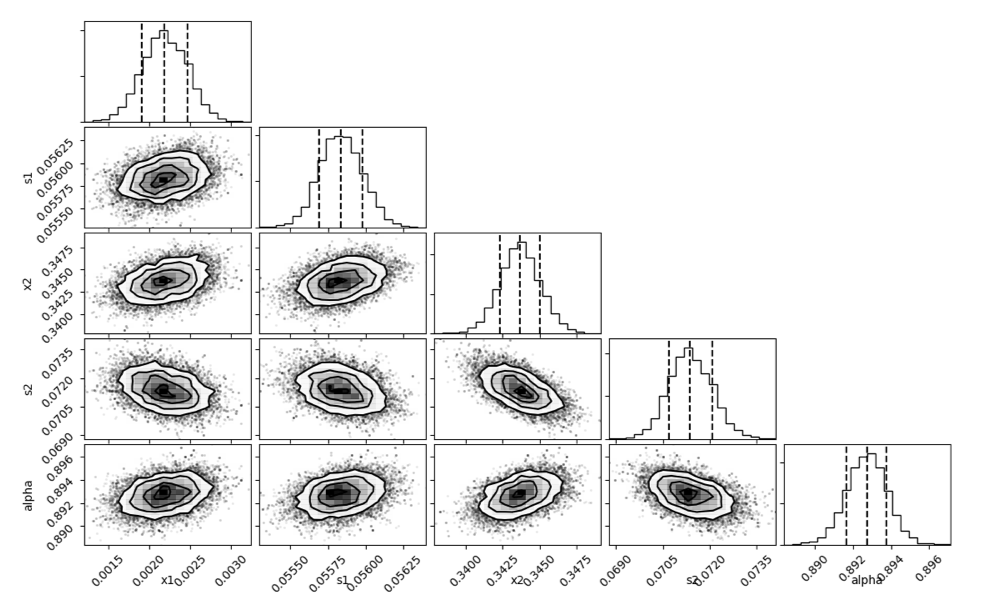
Fig. 5:An example of the emcee fitting procedure for a 2-Gaussian Mixture Model. Each gray line is a different 2-GMM with a different set of parameters. The final output of the fitting procedure would be the set of parameters that maximize the probability of the data given the log likelihood function of a 2-GMM.

The model used in the sampler is a 2-Gaussian Mixture Model with 2-parameter Gaussians and a single mixing parameter. The rationale behind using this type of model and fitting procedure was that it is a fairly conservative model and that the fitting procedure would prevent the problem of overfitting because the sampler would explore the parameter space before choosing a final set of parameters. Moreover, its final choice of parameters depends on whether those parameters maximize the probability of the data given the 2-Gaussian Mixture Model.

Fig. 6:Plot of the walker chains showing that after an initial burn in that the walkers settled down on values that extremized the log likelihood function.
Fig. 7: The contour plots graphs each parameter against one another and shows that that they are normally distributed, as desired.

Fig. 8: The final plot of the 2-Gaussian Mixture Model Markov Chain Monte Carlo (MCMC) implemented by emcee shows that the chosen model is in bad agreement with the data in that it somewhat captures the center and spread of the first peak, but it overestimates the center and spread of the second peak thereby leading to an overestimate of the gain and its uncertainty.

The model used in the fitting procedure did not account for the effects from the truncated interval, and therefore the fit could be improved by using a truncated Gaussian. This is an area for further work as well as exploring the effect of different filters on the signal to noise ratios of the final version of the fitting procedure after the appropriate model is selected.

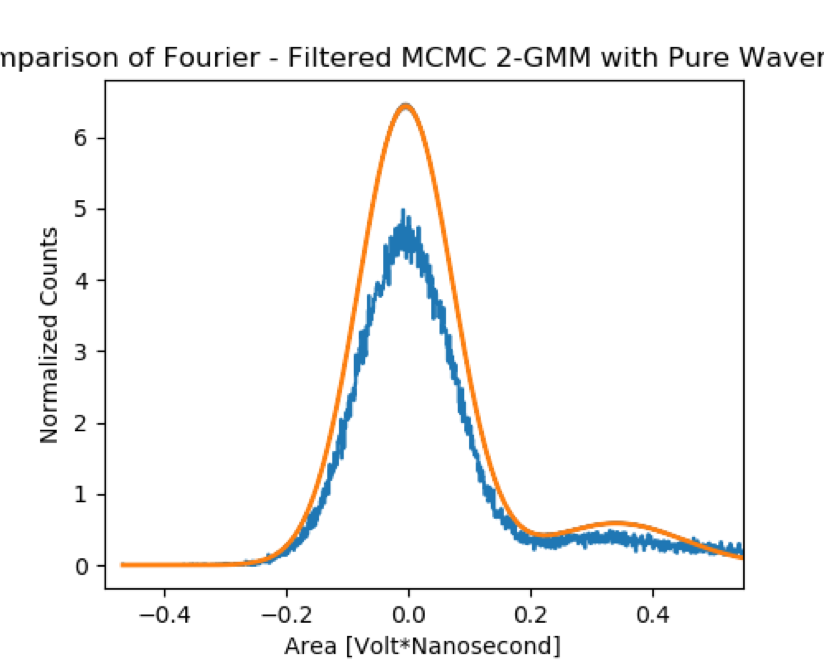
Butterworth filters and Fourier filters were explored to see whether they might improve the signal to noise ratio of the fitting procedure.

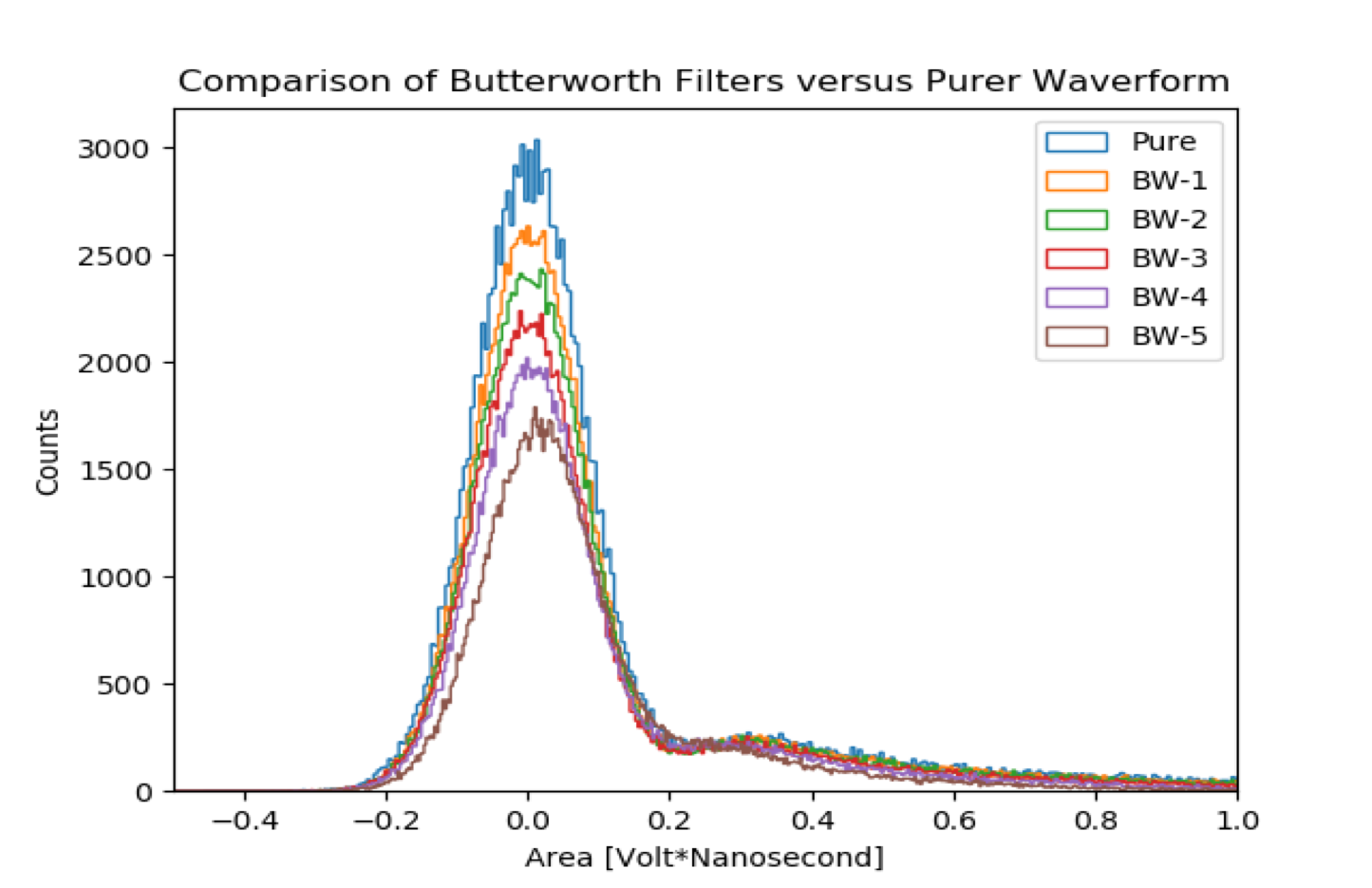
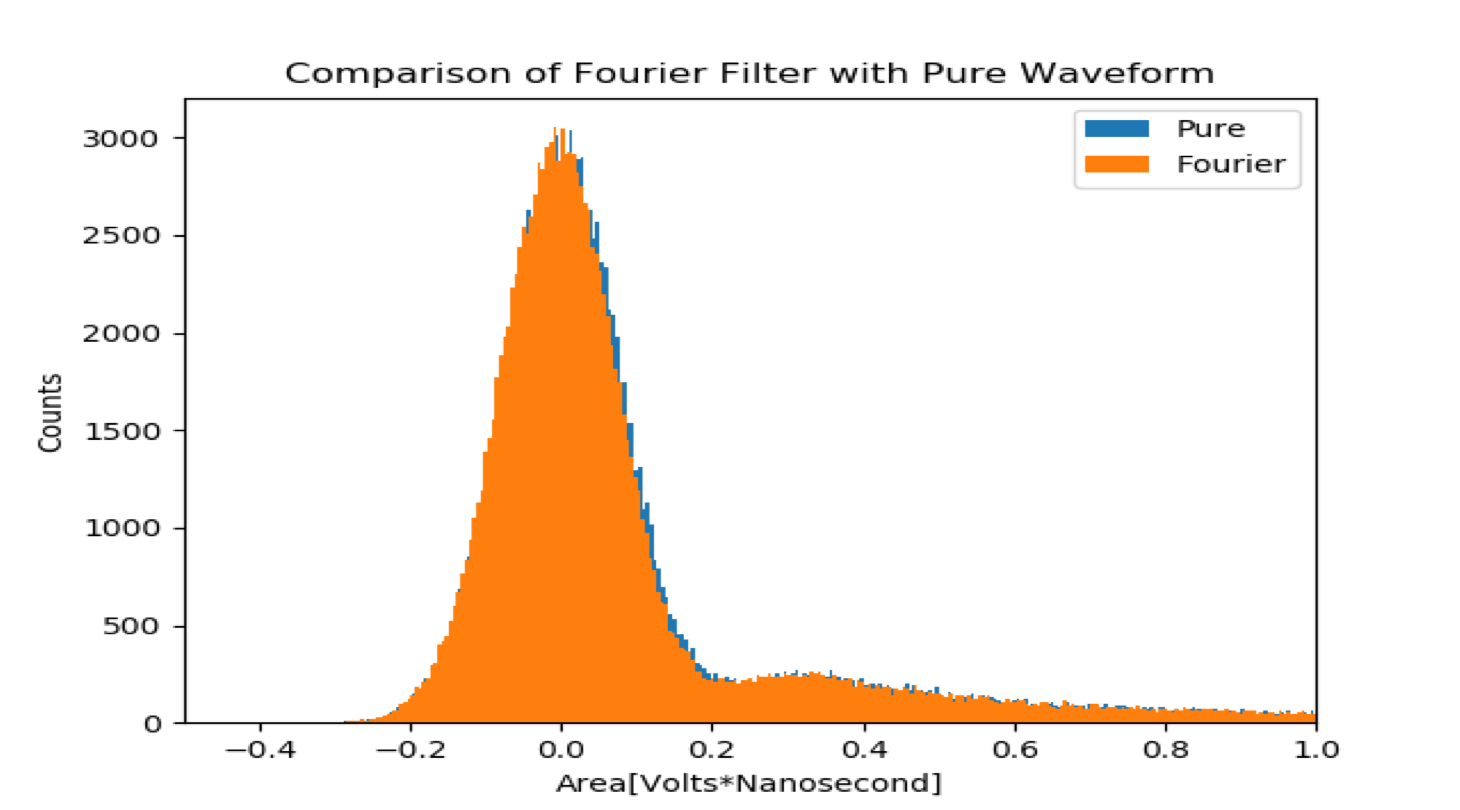
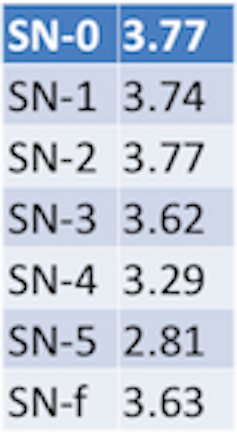
Fig. 9: Comparison of Butterworth filters of varying orders with the pure waveform.
Fig. 10: Comparison of the Fourier filter with the pure waveform.

Unfortunately, because an appropriate model for the data could not be found during the summer, investigation of the filters was never undertaken that time. But initial tests of their viability suggest that they might be useful in optimizing the waveform analysis. According to the Kolmogorov-Smirnov statistic, all filters resulted in resulted statistically significant different distributions, except for the Butterworth filters of order less than three. It is not clear at the present moment whether a Butterworth filter or Fourier filter might offer the better signal to noise ratio.

I continued work later in the fall of 2019 and I was able to apply the 2-Gaussian mixture model to the pure waveform and the different filtered waveforms.

Plot of cut at q = .53.

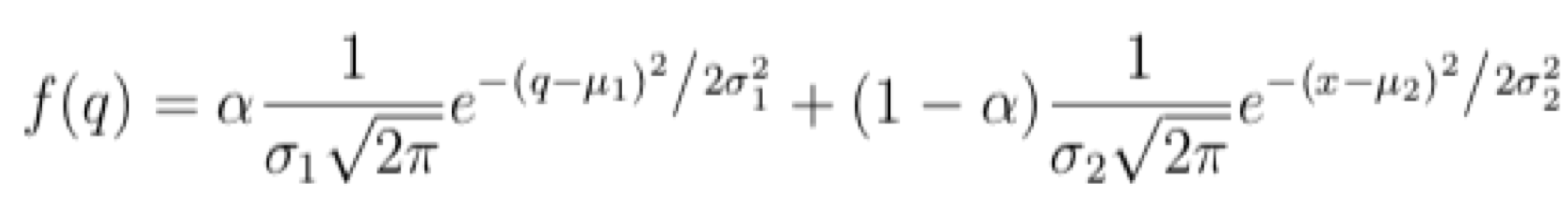
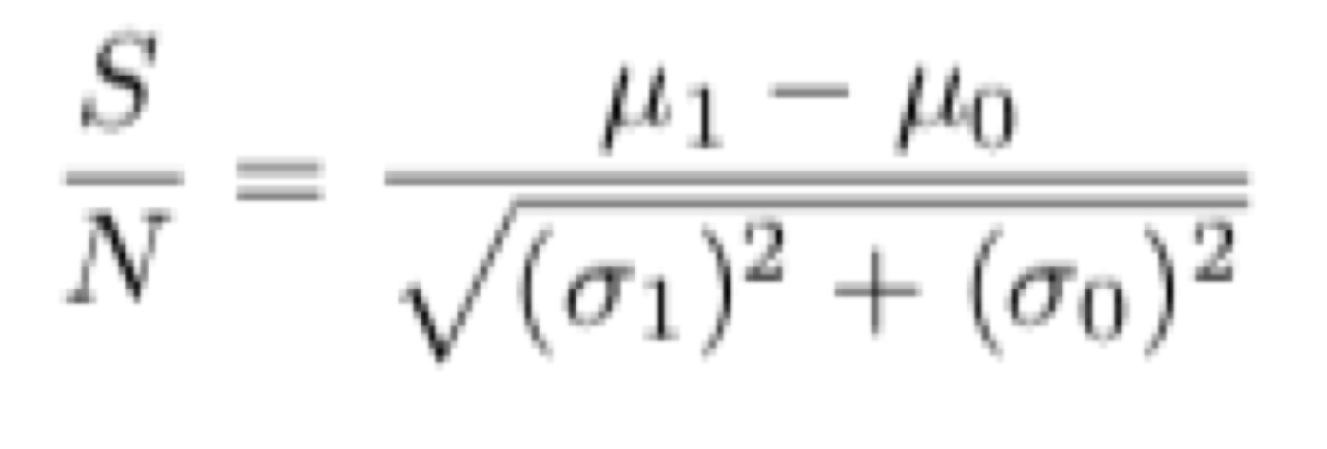
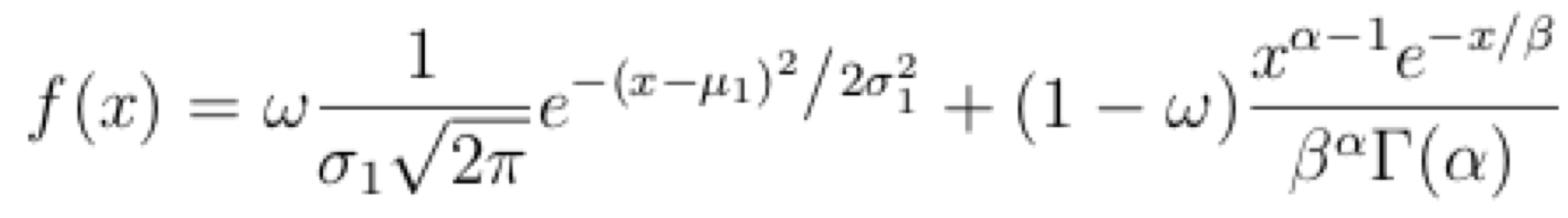
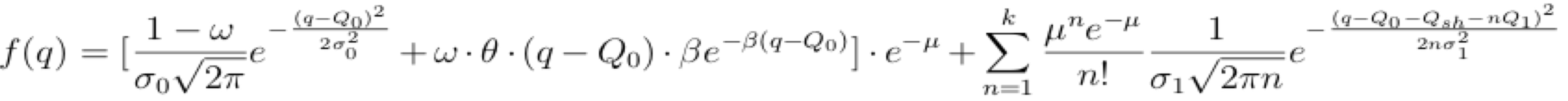
Many thanks to Professor Carl Eric Dahl, Rocco Coppejans, Runze Zhang, Aaron Geller, and Chris Pankow. This material is based upon work supported by the National Science Foundation under Grant No. AST-1757792, a Research Experiences for Undergraduates (REU) grant awarded to CIERA at Northwestern University. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.