What is Dark Matter?
Well...it's complicated. Despite the estimate that over 80% of the universe's matter content is composed of dark matter (DM), most of the physical properties of DM, and its interactions with baryonic matter are not yet understood (Antypas et al. 2022 ; Geraci et al. 2019 ). Attempts to understand DM have culminated in numerous candidates and models across a broad range of astrophysical sub-fields. Of interest to this project, are bosonic ultralight dark matter (UDM) fields. As the name suggests, UDM fields act as classical fields as opposed to particles and have masses under ~10 eV. Most importantly, models of UDM fields allow them to induce oscillations in the fine structure constant (α) and the electron mass (me) (Geraci et al. 2019 ). Such oscillations necessarily create oscillations in the size and spacing of atoms, which manifest themselves in any solid, macroscopic object as a time varying strain of the form (Geraci et al. 2019 ), \begin{equation} h = -\frac{\delta\alpha}{\alpha_0} - \frac{\delta m_e}{m_{e,0}} \end{equation}
How Can We Detect Dark Matter?
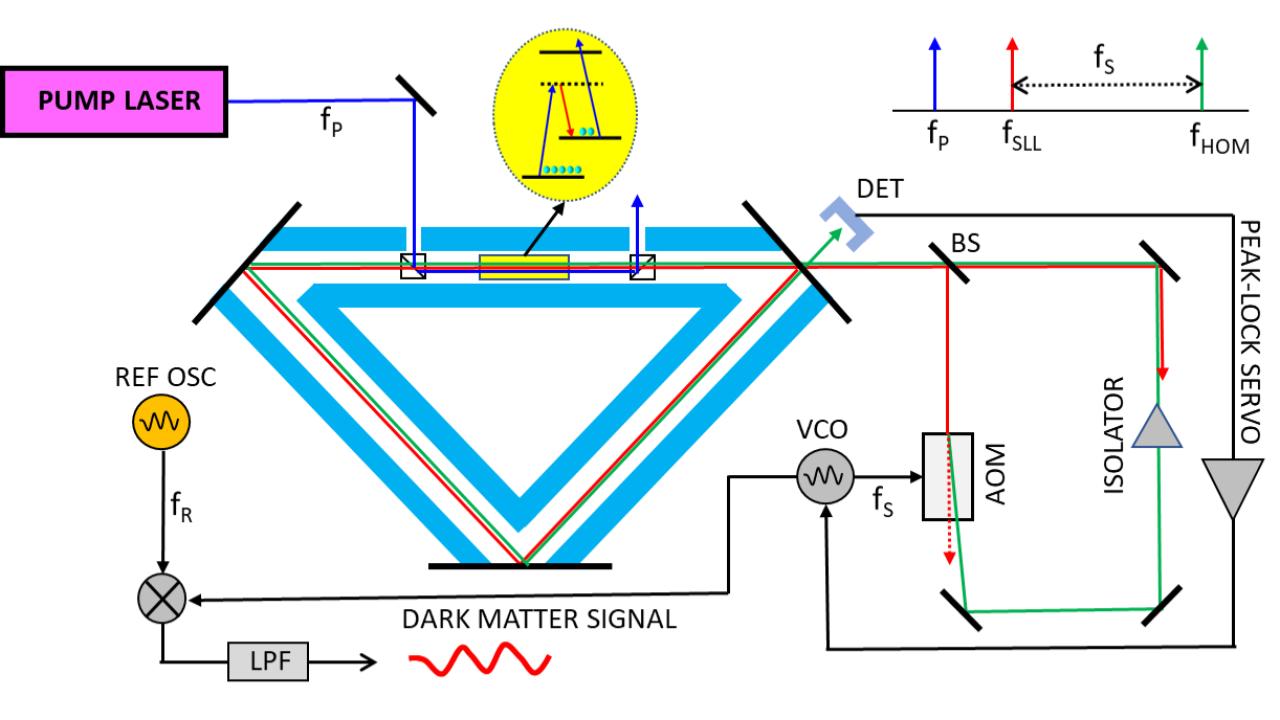
This strain can be measured with a number of feasible experimental setups. One such method, as detailed by Geraci et al. 2019 , makes use of optical cavities. First, consider a standard, rigid optical cavity composed of two highly reflective mirrors separated by some length. As a UDM field passes by the cavity, the length, and consequently the resonant frequency, of the cavity changes. Next we use a secondary optical cavity that has a different shift in resonance frequency for the same passing UDM field. Finally, we shine a laser of frequency ν0 through both cavities, and the differential strain as function of time is given by, \begin{equation} h(t) = \frac{\Delta_{\nu}(t)}{\nu_0} \end{equation} where \(\Delta_{\nu}(t)\) is the differential resonant frequency. At this point, the time varying strain is compared against theoretical models of the strain produced by UDM fields to identify any DM signals. As mentioned earlier, this method requires the use of optical cavities whose resonant frequencies have different sensitivities to the strain produced by a UDM field. To achieve this, Geraci et al. 2019 proposes a method in which one of the cavities is created by suspending the mirrors on springs, similar to LIGO, which in turn suppresses changes in the mirror spacing relative to the other, rigid cavity. However, we instead make use of a subluminal laser , which is a laser whose resonant frequency is highly resistant to changes in cavity length ( Yablon et al. 2016 ). A model of the proposed dark matter detector is shown in Figure 1.