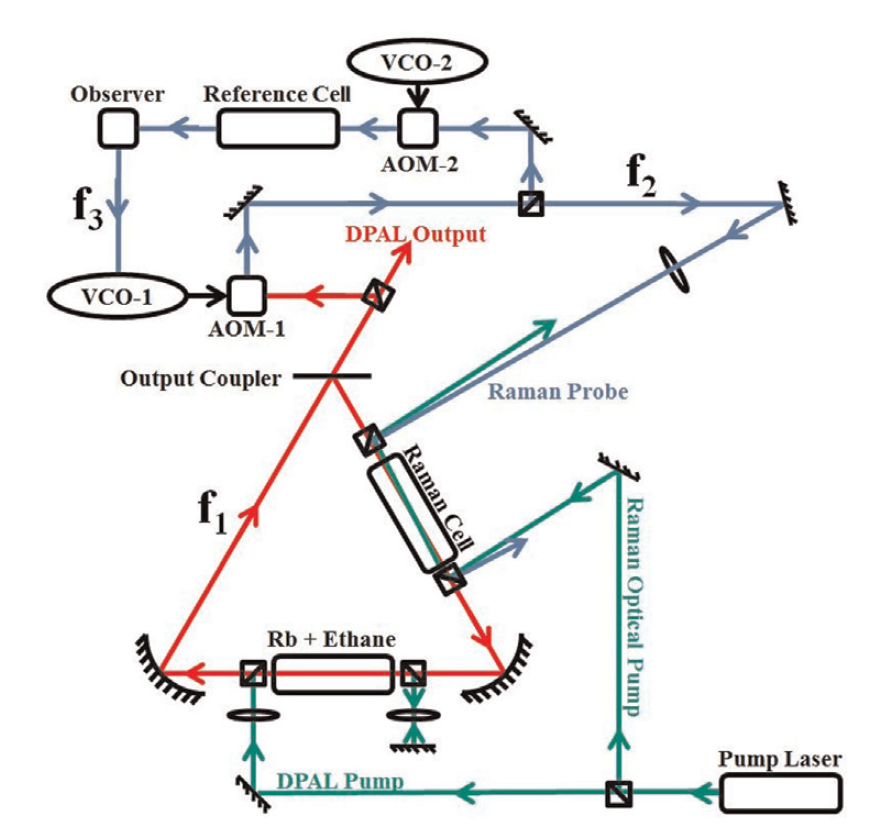
An Overview of Subluminal Lasers
Our dark matter detector makes use of a subluminal laser, which is a laser whose resonant frequency is highly resistant to changes in cavity length. A subluminal laser is realized by using a cavity containing a slow light medium, which is a medium in which the group velocity of the laser is smaller than the speed of light in vacuum. The factor by which the resonant frequency is resistant to a change in cavity length is known as the Sensitiviy Suppression Factor (SSF) and is simply the ratio between resonant frequency shift in the subluminal laser and the frequency shift of an empty cavity. It has been theoretically and experimentally demonstrated that the SSF of a subluminal laser is roughly equal to the index of refraction ng of the intra-cavity medium ( Yablon et al. 2016 ). Subluminal lasers are therefore excellent candidates our purposes since a high index of refraction is relatively simple to achieve experimentally. In fact, a subluminal laser with an index of refraction (and consequently SSF) of 663 has been achieved experimentally ( Yablon et al. 2016 )! However, the exact physics of a subluminal laser are quite complex, and therefore require numerical modeling to understand fully. A strong model of subluminal lasers is necessary in order to find the best parameters for a future DM detector.
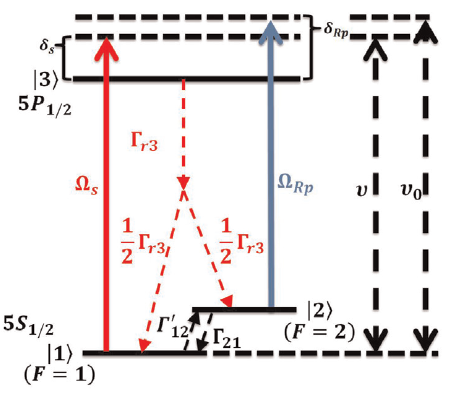
The Gain Medium Inside Our Subluminal Laser
The gain in our subluminal laser is produced in a Rubidium (Rb) vapor cell via a Raman transition, which works as follows. The Rb atom is modeled as a four level system, in which two ground states, A and B, are coupled to a pair of optically excited states, C and D. An optical pump beam couples A to D, which decays back to A and B, thus p roducing a population inversion among A and B. A Raman pump laser couples B to C in a detuned manner. A probe beam that couples A to C then experiences Raman gain, which is maximized when the energy difference between the pump and the probe matches that between A and B. This gain produced in this manner can be very narrow spectrally, as needed for the subluminal laser. A diagram illustrating the Raman gain process is shown in Figure 3.